Para realizar a adição e a subtração de fração, é necessário analisar se os denominadores são iguais ou diferentes. Se os denominadores forem iguais, realizamos a adição ou a subtração com os numeradores. Se os denominadores forem diferentes, igualamos os denominadores e realizamos a operação. Para igualar os denominadores podemos utilizar o MMC ou o método prático.
Leia também: Como transformar uma fração em uma porcentagem
Tópicos deste artigo
- 1 - Como fazer adição de frações?
- 2 - Como fazer subtração de frações?
- 3 - Adição e subtração de frações mistas
- 4 - Exercícios resolvidos sobre adição e subtração de frações
Como fazer adição de frações?
Para realizar a adição de fração, dividiremos o método em dois casos. O primeiro é quando os denominadores são iguais, o segundo é quando os denominadores são diferentes.
- Denominadores iguais: se as frações têm o mesmo denominador, você pode somar apenas os numeradores e manter o denominador constante.
\(\frac{2}{8}+\frac{3}{8}=\frac{5}{8}\)
\(\frac{2}{5}+\frac{2}{5}=\frac{4}{5}\)
- Denominadores diferentes: a soma de frações com denominadores diferentes envolve trazer as frações para um denominador comum antes de realizar a operação.
Primeiro encontraremos o mínimo múltiplo comum (MMC) dos denominadores e, em seguida, ajustaremos as frações para que elas tenham esse denominador comum. Depois disso, os numeradores podem ser somados e o resultado é dividido pelo denominador comum.
Exemplo 1:
\(\frac{1}{2}+\frac{2}{3}\ \)
Primeiro encontraremos o MMC de 2 e 3.
2, 3 | 2
1, 3 | 3
1, 1 | 2 ⋅ 3 = 6
Como o MMC é 6, multiplicaremos o numerador e o denominador de cada uma das frações, de modo que os denominadores sejam iguais a 6. Assim, dividiremos o MMC pelo denominador da fração.
\(6 : 2 = 3\)
Multiplicaremos o resultado pelo numerador e o denominador da fração:
\(\frac{1\cdot3}{2\cdot3}=\frac{3}{6}\)
Repetindo o mesmo processo para a segunda fração, temos que:
\(6 : 3 = 2\)
Multiplicando o numerador e o denominador por 2 na segunda fração:
\(\frac{2\cdot2}{3\cdot2}=\frac{4}{6}\)
Note agora que as frações possuem o mesmo denominador. Somando os numeradores, temos que:
\(\frac{3}{6}+\frac{4}{6}=\frac{7}{6}\)
Exemplo 2:
\(\frac{2}{3}+\frac{4}{8}\ \)
Calculando o MMC:
\(3, 8 | 2 \)
\(3, 4 | 2\)
\(3, 2 | 2\)
\(3, 1 | 3 \)
\(1, 1 | 3\cdot2^3=3\cdot8=24\)
Sabemos que o MMC entre 3 e 8 é 24.
Na primeira fração temos que:
\(24 : 3 = 8\)
\(\frac{2\cdot8}{3\cdot8}=\frac{16}{24}\)
Na segunda fração:
\(24 : 8 = 3\)
\(\frac{4\cdot3}{8\cdot3}=\frac{12}{24}\)
Logo:
\(\frac{16}{24}+\frac{12}{24}=\frac{28}{24}\)
Podemos simplificar a fração, portanto:
\(\frac{{28}^{:4}}{{24}_{:4}}=\frac{7}{6}\)
-
Método prático (borboleta) para adição de fração
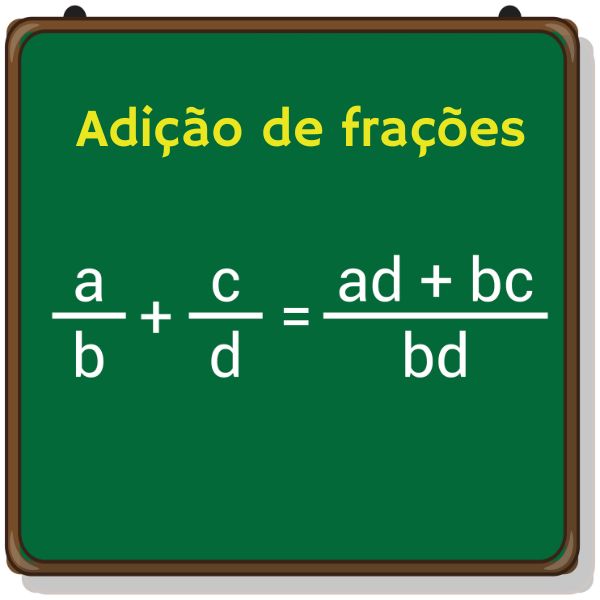
Exemplos:
\( a)\ \frac{3}{7}+\frac{4}{5}=\frac{3\cdot5+7\cdot4}{7\cdot5}=\frac{15+28}{35}=\frac{43}{35}\)
\(b)\ \frac{2}{5}+\frac{4}{9}=\frac{2\cdot9+5\cdot4}{7\cdot5}=\frac{18+20}{45}=\frac{38}{45}\)
Leia também: Como multiplicar frações
Como fazer subtração de frações?
Subtrair frações é semelhante à adição de frações, com a diferença de que aqui separaremos as peças de um quebra-cabeça para formar um todo menor. Aqui estão os passos:
- Denominadores iguais: se as frações têm o mesmo denominador, você pode subtrair apenas os numeradores e manter o denominador constante.
\(\frac{5}{8}-\frac{2}{8}=\frac{5-2}{8}=\frac{3}{8}\)
\(\frac{3}{5}-\frac{2}{5}=\frac{1}{5}\)
- Denominadores diferentes: a subtração de frações com denominadores diferentes envolve trazer as frações para um denominador comum antes de realizar a operação.
A primeira maneira é encontrar o mínimo múltiplo comum (MMC) dos denominadores e, em seguida, ajustar as frações para que elas tenham esse denominador comum. Depois disso, os numeradores podem ser somados e o resultado é dividido pelo denominador comum.
Exemplo 1:
\(\frac{3}{4}-\frac{2}{3}\ \)
Sabemos que o MMC entre 4 e 3 é 12, logo temos:
\(\frac{9}{12}-\frac{8}{12}=\frac{1}{12}\)
Exemplo 2:
\(\frac{2}{3}-\frac{4}{8}\ \)
Sabemos que o MMC entre 3 e 8 é 24, logo temos:
\(\frac{16}{24}-\frac{12}{24}=\frac{4}{24}\)
Simplificando por 4, temos \(\frac{1}{6}\).
-
Método prático (borboleta) para subtração de frações

Exemplos:
\(\frac{5}{7}-\frac{3}{5}=\frac{5\cdot5-7\cdot3}{7\cdot5}=\frac{25-21}{35}=\frac{4}{35}\)
\(\frac{3}{5}-\frac{4}{9}=\frac{3\cdot9-5\cdot4}{7\cdot5}=\frac{27-20}{45}=\frac{7}{45}\)
Adição e subtração de frações mistas
A fração mista é composta por uma parte inteira e uma parte fracionária. Para realizar a soma ou a subtração, primeiro somam-se ou subtraem-se as partes inteiras, e, em seguida, realiza-se a operação com as partes fracionárias. Se necessário, a fração resultante pode ser simplificada.
Exemplos:
\(2\frac{1}{3}+3\frac{2}{5}=\left(2+3\right)+\left(\frac{1}{3}+\frac{2}{5}\right)=5+\frac{11}{15}=5\frac{11}{15}\)
\(4\frac{1}{2}-3\frac{2}{5}=\left(4-3\right)+\left(\frac{1}{2}-\frac{2}{5}\right)=1+\frac{1}{10}=1\frac{1}{10}\)
Leia também: Como dividir frações
Exercícios resolvidos sobre adição e subtração de frações
Questão 1
Um bolo de milho foi dividido em 12 pedaços iguais. João comeu 3/12, e Maria comeu 4/12. Quanto do bolo foi consumido no total?
A) 4/12
B) 5/12
C) 6/12
D) 7/12
E) 8/12
Resolução:
Alternativa D
Como o denominador é o mesmo, temos que:
\(\frac{3}{12}+\frac{4}{12}=\frac{3+4}{12}=\frac{7}{12}\)
Questão 2
Agnaldo tinha \(\frac{2}{5}\) de uma pizza marguerita, e seu irmão comeu \(\frac{1}{8}\) dela. Quanta pizza Agnaldo tem agora?
A) \( \frac{11}{40}\)
B) \( \frac{3}{40}\)
C) \( \frac{21}{40}\)
D) \( \frac{2}{40}\)
Resolução:
Alternativa A
Agnaldo tinha \(\frac{2}{5}\) da pizza.
Seu irmão comeu \(\frac{1}{8}\).
Para encontrar o quanto Agnaldo tem agora, subtraímos as frações:
\(\frac{2}{5}-\frac{1}{8}\)
Primeiro, encontramos o denominador comum, que é 40 neste caso:
\(\frac{2}{5}=\frac{16}{40}\)
\(\frac{1}{8}=\frac{5}{40}\)
Subtraindo as frações:
\(\frac{16}{40}-\frac{5}{40}=\frac{11}{40}\)
Agnaldo tem agora \(\frac{11}{40}\) da pizza restante.
Fontes:
MCLEOD, S. A. Teoria das Frações: Uma Abordagem Lúdica. 2ª ed. São Paulo: Editora Matemática Divertida, 2020.
POSSANI, C. Frações: Ensinando Matemática com Jogos e Atividades. 1ª ed. São Paulo: Editora Contexto, 2016.


