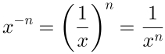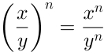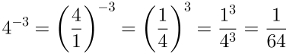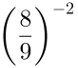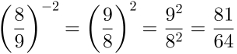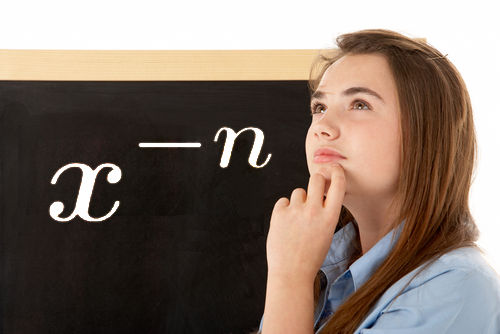
Potência com expoente negativo
Matemática
Potências são sequências de produtos com todos os fatores iguais. Quando o expoente delas é negativo, é preciso recorrer às propriedades de potências.
Potências são o resultado de produtos em que todos os fatores são iguais. Elas são representadas de maneira única por meio de uma base, que é o número multiplicado, e de um expoente, que é a quantidade de vezes que esse número é multiplicado. Quando o expoente de uma potência é negativo, precisamos usar algumas das propriedades de potência para conseguir calculá-la. Uma dessas propriedades é a potência de frações, e a outra é a própria potência com expoente negativo.
Potências com expoente negativo
Quando uma potência possui expoente negativo, a propriedade usada para calculá-la é a seguinte:
Essa propriedade geralmente é lida da seguinte maneira: quando uma potência possui expoente negativo, inverta sua base e também o sinal do expoente. Assim, para resolver potências cujo expoente é negativo, proceda da seguinte maneira:
-
Escreva a base da potência na forma de fração;
-
Inverta a base e também o sinal do expoente;
-
Faça os cálculos e, se necessário, com as propriedades de potência.
Não pare agora... Tem mais depois da publicidade ;)
Potência de frações
São potências cuja base é uma fração. Para resolvê-las, basta elevar separadamente numerador e denominador ao expoente dessa potência. Observe:
Na potência acima, calculamos xn e yn para obter o resultado.
1º Exemplo – Calcule a potência de expoente negativo a seguir:
Solução: primeiramente, escrevemos a base da potência em forma de fração. Depois, aplicamos a propriedade de potências com expoente negativo e, por fim, resolvemos cada potência separadamente. Observe:
2º Exemplo – Calcule a potência de expoente negativo a seguir:
Solução: faça exatamente o mesmo que foi feito no exemplo anterior. A única diferença é que não é necessário escrever a base em forma de fração, pois ela já está assim.
Por Luiz Paulo Moreira
Graduado em Matemática
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SILVA, Luiz Paulo Moreira. "Potência com expoente negativo"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/potencia-com-expoente-negativo.htm. Acesso em 20 de janeiro de 2022.
Qual dos resultados a seguir é solução da potência 10– 6?
a) 0,01
b) 0,001
c) 0,0001
d) 0,00001
e) 0,000001
A respeito das propriedades de potências, qual das seguintes alternativas está correta?
a) No produto entre duas potências de mesmo expoente, conserva-se a base e somam-se os expoentes.
b) Na divisão entre duas potências de mesmo expoente, conserva-se a base e subtraem-se os expoentes.
c) Em uma potência de expoente negativo, inverte-se a base e troca-se o sinal do expoente.
d) Em uma potência de potência, conserva-se a base e somam-se os expoentes.
e) N. D. A.
Mais Questões
Proibida a reprodução total ou parcial sem prévia autorização (Inciso I do Artigo 29 Lei 9.610/98)