O que é o conjunto dos números irracionais?

Os conjuntos numéricos são agrupamentos de números que os separam de acordo com suas características mais importantes e também levando em consideração seu processo de criação. O conjunto dos números irracionais é aquele cujos elementos são números decimais que não podem ser resultado da divisão entre dois números inteiros. Essa definição é o oposto da definição de número racional: qualquer número que pode ser escrito na forma de fração.

Breve histórico

Os números racionais foram criados a partir da necessidade de dividir objetos entre pessoas. Mais adiante foi criada a reta numérica, em que cada ponto faz correspondência com um único número real. Ao analisá-la mais a fundo, os matemáticos perceberam que haviam “buracos” na reta numérica e que não existiam números racionais que se relacionassem com esses pontos. Houve inicialmente uma desconfiança de que existiam muito mais números do que apenas os números racionais (conjunto que contém os números naturais e inteiros).

Com o tempo, percebeu-se que essas lacunas deveriam ser preenchidas com números decimais infinitos e não periódicos. Pouco a pouco também se percebeu que alguns desses decimais poderiam ser representados por raízes não exatas.

Representação de irracionais na reta numérica

Desenhe um quadrado de lado 1, com um dos vértices na origem de uma reta numérica, e calcule a medida de sua diagonal pelo teorema de Pitágoras:

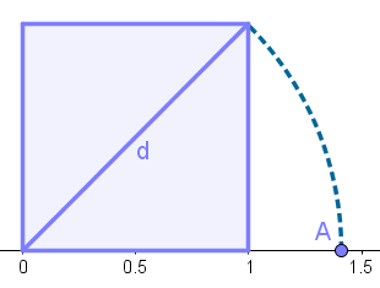
Cálculo da diagonal do quadrado de lado 1 para representar o número irracional √2

d² = 1² + 1²

d² = 1 + 1

d² = 2

d = √2

Sabendo que a diagonal desse quadrado mede √2, basta utilizar um compasso para “transportar” essa medida para a reta numérica. Logo abaixo do quadrado, coloque a ponta fixa do esquadro no início da diagonal e a ponta móvel no fim. Gire o compasso, marcando o local onde essa ponta se encontra com a reta numérica.

Quais números são irracionais?

Os números irracionais são aqueles que não são racionais. Assim, seus representantes são:

• Todos os decimais infinitos não periódicos

Observe que o número abaixo não é periódico, mas pode-se dizer que prossegue infinitamente.

1,2345678910111213141516171819202122...

Alguns desses números podem ser representados por raízes não exatas e outros são tão importantes que ganharam “nome”.

Números irracionais notáveis

Dentro do conjunto dos números irracionais existem alguns elementos que foram usados por grandes matemáticos da Antiguidade. Destacaremos aqui apenas dois deles: π e φ.

O número irracional π é obtido no resultado da divisão entre o comprimento e o diâmetro de uma circunferência e representa o número que se inicia com as seguintes casas decimais:

3,14159265358979...

Como esse número possui infinitas casas decimais e não é uma dízima periódica, ele é irracional.

O número áureo, representado pela letra grega φ, refere-se à proporção perfeita e é proporcional a:

1 + √5
2

Assim, o número φ = 1,6180339... também é um número irracional.

Por Luiz Paulo Moreira
Graduado em Matemática