Número quadrado perfeito

Existem alguns padrões na Matemática que nos despertam a curiosidade e podem estar relacionados com alguma sequência numérica. Quando vemos números enfileirados, logo nos questionamos sobre o seu padrão de formação. Veja os números a seguir:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100 …

Qual deve ser a lógica dessa sequência? A resposta está no número quadrado perfeito. Entenda que um número será quadrado perfeito quando ele for um número inteiro e o seu quadrado gerar outro número inteiro positivo. Veja:

1² = 1 . 1 = 1
2² = 2. 2 = 4
3² = 3 . 3 = 9
4² = 4 . 4 = 16
5² = 5 . 5 = 25
6² = 6 . 6 = 36
7² = 7 . 7 = 49
8² = 8 . 8 = 64
9² = 9 . 9 = 81
10² = 10 . 10 = 100
.
.
.

Após observar esses cálculos, é possível determinar um padrão de formação, que é dado por:

n² = n . n = a
n² = a

• (n²) é o número inteiro positivo;

• (n . n) é o produto de termos numéricos idênticos, que são positivos;

• (a) é o número quadrado perfeito.

Exitem algumas regras práticas que ajudam a identificar os números que são quadrados perfeitos.

Primeira Regra: Somente o número quadrado perfeito possui raiz quadrada exata.

Exemplos:

Veja o cálculo da raiz quadrada dos números a seguir:

Segunda Regra: Quando o número é quadrado perfeito, ele não possui como último algarismo os seguintes números: 2, 3, 7 e 8.

Terceira Regra: Todo número quadrado perfeito que for par possuirá raiz quadrada par. Lembre-se de que um número é considerado par quando for dividido por dois e resultar em um número inteiro.

Exemplos:

Verifique se os números 4, 9 e 16 são pares e calcule a raiz quadrada deles:

4 : 2 = 2 → Temos que 4 é um número par;
9 : 2 = 4,5 → O número 9 não é par;
16 : 2 = 8 → O número quadrado perfeito 16 é par.

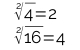
Quarta Regra: Um número par será quadrado perfeito se, ao ser dividido por 4, resultar em um número inteiro.

Quinta Regra: Todo número quadrado perfeito que é ímpar possui raiz quadrada ímpar. Um número será ímpar quando ele for dividido por dois e resultar em um número que não é inteiro, ou seja, um número decimal.

Exemplos

Considere os números 100 e 121. Verifique qual é ímpar e calcule a sua raiz quadrada.

100 : 2 = 50 → 100 é par;
121 : 2 = 60,5 → 121 é ímpar.

A raiz quadrada de 121 é 11. Sendo assim, a quinta regra é valida, pois número quadrado perfeito ímpar possui raiz quadrada ímpar.

Sexta Regra: Ao dividir um número quadrado perfeito ímpar por oito, o resto sempre será o número 1.

Exemplos:

Verifique se os números 9 e 25 deixam resto 1 ao serem divididos por 8:

9 | 8
8  1
1

25 | 8
24  3
1

Observando as divisões acima, verificamos que a sexta regra é valida para os números que são ímpares e quadrados perfeitos.

Por Naysa Oliveira
Graduada em Matemática