Conhecemos como MMC o mínimo múltiplo comum de dois ou mais números. Encontrar o MMC entre dois números é procurar o menor número múltiplo de dois ou mais números simultaneamente. Para encontrar o MMC entre dois números, podemos fazer uma lista dos múltiplos de cada um deles até achar um que seja comum a ambos, ou então utilizar o método de decomposição em fatores primos ou até mesmo o de fatoração sucessiva. Existem propriedades importantes para o mínimo múltiplo comum.
Leia também: Dicas e macetes para cálculos de divisão
Tópicos deste artigo
- 1 - Resumo sobre MMC
- 2 - Videoaula sobre mínimo múltiplo comum (MMC)
- 3 - O que é o MMC?
- 4 - Como calcular o MMC?
- 5 - Propriedades do MMC
- 6 - MMC em frações
- 7 - Diferença entre MMC e MDC
- 8 - Exercícios resolvidos sobre mínimo múltiplo comum (MMC)
Resumo sobre MMC
-
O mínimo múltiplo comum é conhecido como MMC.
-
O MMC entre dois ou mais números é o menor número múltiplo desses números simultaneamente.
-
Existem métodos diferentes para encontrar o MMC.
-
O MMC possui propriedades importantes.
Videoaula sobre mínimo múltiplo comum (MMC)
O que é o MMC?
Conhecemos como MMC o mínimo múltiplo comum entre dois ou mais números. Encontrar o MMC entre dois números é identificar o menor número inteiro diferente de zero e múltiplo de ambos simultaneamente. Para compreender o que é o MMC, é fundamental saber o que são os múltiplos de número.
Conhecemos como múltiplos de um número o produto obtido quando multiplicamos um número natural por outro número natural.
Exemplo 1:
M(12) = {0, 12, 24, 36, 48, 60, 72, 84, 96…}
Note que o conjunto dos números múltiplos de 12 é formado pelos resultados de 12 vezes 0, 12 vezes 1, 12 vezes 2, e assim sucessivamente. O conjunto de múltiplos é infinito.
Exemplo 2:
Vejamos agora os múltiplos de 14:
M(14) = {0, 14, 28, 42, 56, 70, 84, 98, 112…}
Podemos encontrar o mínimo múltiplo comum entre esses dois números (12, 14), para isso, basta analisar as duas listas de múltiplos e procurar o menor número inteiro diferente de zero e que seja múltiplo dos dois.
MMC(12, 14)
M(12) = {0, 12, 24, 36, 48, 60, 72, 84, 96…}
M(14) = {0, 14, 28, 42, 56, 70, 84, 98, 112…}
MMC(12, 14) = 84
Leia também: Macetes e dicas de matemática para o Enem
Como calcular o MMC?
Para calcular o MMC entre dois ou mais números, existem vários métodos. Os que mais se destacam são três, apresentados a seguir.
-
1º método - comparação dos múltiplos
O primeiro deles é o que nós utilizamos anteriormente para encontrar o MMC entre 12 e 14: escrever a lista de múltiplo de cada um dos números e encontrar o menor múltiplo em comum entre eles.
Exemplo: MMC(10, 15)
M(10) = {0, 10, 20, 30…}
M(15) = {0, 15, 30…}
MMC(10, 15) = 30
Acontece que esse método é pouco prático quando há mais números, ou então, quando os números são maiores, muitas vezes encontrar o MMC escrevendo a lista de múltiplos de cada um dos números pode ser bastante trabalhoso.
2º método - decomposição em fatores primos
O método de decompor os números em fatores primos facilita encontrar os múltiplos em comum quando os números são maiores.
Os números que não são primos podem ser escritos como o produto entre números primos. Esse método consiste em reescrever os números na forma fatorada e multiplicar os fatores com os seus maiores expoentes.
Exemplo:
Encontre o MMC(36, 40):
Primeiro vamos escrever esses números na sua forma fatorada:
36 = 2² · 3²
40 = 2³ · 5
Os fatores encontrados na decomposição foram 2, 3 e 5. Vamos realizar a multiplicação entre eles com os seus respectivos exponentes. Note que o 2 apareceu em ambos, nesse caso, escolhemos o maior expoente:
MMC(36, 40) = 2³ · 3² · 5
MMC(36, 40) = 8 · 9 · 5
MMC(36, 40) = 360
-
3º método - método das divisões sucessivas
O terceiro método é o mais utilizado e é conhecido como método prático do MMC ou método das divisões sucessivas. Como o nome sugere, nele se realiza divisões sucessivas com esses números simultaneamente para encontrar os fatores cujo o produto será o MMC.
Exemplo:
Calcule MMC(48, 84).
1º passo: montar o algoritmo e encontrar o menor número primo que divide pelo menos um dos dois números.

2º passo: realizar a divisão desses números por 2 e escrever o resultado logo abaixo:
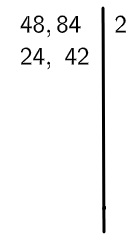
3º passo: com os resultados encontrados, repetiremos o processo, dividindo-os novamente por 2:
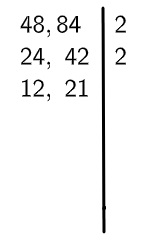
4º passo: note que 2 não divide o 21, mas ainda divide o 12, então escreveremos o 2 como fator, mas realizaremos somente a divisão que tem resultado inteiro, repetindo o processo até que não tenha mais nenhum número divisível por 2.
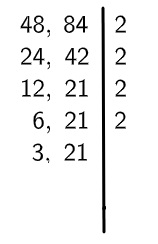
5º passo: encontraremos agora o próximo número primo que divide qualquer um dos dois números, que, no caso, é o 3, e realizaremos a divisão.
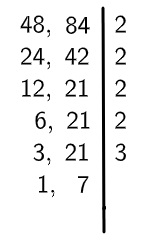
6º passo: como 3 não divide mais nenhum dos dois números, então encontraremos o próximo número que divide qualquer um dos dois números, que no caso é 7.
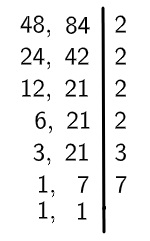
7º passo: agora que não é mais possível dividir, calculamos o produto entre os números encontrados para encontrar o MMC.
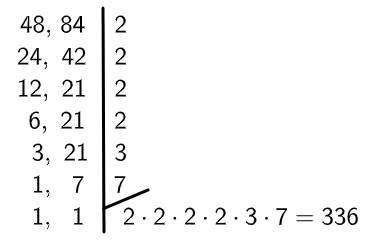
Então, o MMC(48, 84) = 336.
Leia também: Três conceitos básicos de matemática para o Enem
Propriedades do MMC
Existem algumas propriedades importantes do MMC:
1ª propriedade: o MMC entre dois números primos entre si é igual ao produto entre esses dois números.
Exemplo:
MMC(10, 9)
Note que os divisores de 10 são D(10) = {1, 2, 5, 10} e os divisores de 9 são {1, 3, 9}. Sendo assim, não existe nenhum divisor comum entre esses números, logo, temos que:
MMC(10, 9) = 10 × 9 = 90
2ª propriedade: quando um dos números de que queremos encontrar o MMC é múltiplo do outro, então o MMC entre esses números será o maior deles.
Exemplo:
MMC(4, 12)
M(6) = {0, 4, 8, 12 , 18...}
M(18) = {0, 12…}
MMC(4, 12) = 12
MMC em frações
Utilizamos o MMC para igualar os denominadores de frações, a fim de que seja possível calcular a adição ou a subtração entre duas frações.
Para calcular a soma de duas frações com denominadores distintos, é necessário calcular o mínimo múltiplo comum dos denominadores, a fim de escrever frações equivalentes que possuam o mesmo denominador e, assim, ser possível realizar a soma.
Exemplo:
![]()
Primeiro encontraremos o MMC(9, 5). Como eles são primos entre si, basta multiplicar 9 × 5 = 45, então, temos que:
MMC(9, 5) = 45
Encontrado o MMC, agora precisamos analisar as frações. Na primeira, para que o denominador seja igual a 45, é necessário multiplicar por 5 tanto o numerador quanto o denominador.
Já na segunda fração, como o denominador igual a 5, é necessário multiplicar o numerador e o denominador por 9. Após igualar os denominadores, é possível realizar a soma entre as frações:
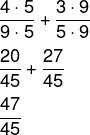
Veja também: Três erros comuns na simplificação de fração algébrica
Diferença entre MMC e MDC
Conhecemos o mínimo múltiplo comum (MMC), mas existe também o máximo divisor comum (MDC). Como o nome sugere, o máximo divisor comum é o maior número divisor de dois ou mais números ao mesmo tempo.
Exemplo:
MDC(18, 27)
Dessa vez, escreveremos a lista de divisores de cada um desses números:
D(18) = {1, 2, 3, 6, 9, 18}
D(27) = {1, 3, 9, 27}
MDC(18, 27) = 9
-
Videoaula sobre MMC e MDC
Exercícios resolvidos sobre mínimo múltiplo comum (MMC)
Questão 1 - (IFG 2019) Antônio realiza atividades físicas regularmente, entre as modalidades de corrida, ciclismo e natação. Ele corre a cada três dias, pedala dia sim e dia não, e nada de quatro em quatro dias. Certa vez, coincidiu de realizar essas três atividades físicas no mesmo dia. É correto afirmar que essa coincidência voltará a ocorrer daqui a
A) 06 dias.
B) 08 dias.
C) 10 dias.
D) 12 dias.
Resolução
Alternativa D
Queremos o MMC(2, 3, 4).
Listando os múltiplos de cada um deles até encontrar o primeiro que seja comum aos três, temos que:
M(2) = {0, 2, 4, 6, 8, 10, 12...}
M(3) = {0, 3, 6, 9, 12...}
M(4) = {0, 4, 8, 12…}
Então, o MMC(2, 3, 4) = 12.
Questão 2 - Em um conselho regional, o presidente é eleito a cada 4 anos, o secretário, a cada 3 anos, e o coordenador geral, a cada 2 anos. Se em 2020 houve eleições para os três cargos simultaneamente, das opções abaixo, em que ano isso ocorrerá novamente?
A) 2028
B) 2030
C) 2032
D) 2034
Resolução
Alternativa C
Calculando o MMC(4, 3, 2), temos que:
M(4) = {0, 4, 8, 12…}
M(3) = {0, 3, 6, 9, 12…}
M(2) = {0, 2, 4, 6, 8, 10, 12…}
Então, temos que: MMC(4, 3, 2) = 12.
Desse modo, a eleição para esses 3 cargos ocorrerá simultaneamente em 12 anos, 2020 + 12 = 2032.




