A motivação para o estudo das operações entre conjuntos vem da facilidade que elas trazem para a resolução de problemas numéricos do cotidiano. Utilizaremos algumas ferramentas gráficas, como o diagrama de Venn-Euler, para definir as principais operações entre dois ou mais conjuntos, sendo elas: união de conjuntos, intersecção de conjuntos, diferença de conjuntos e conjunto complementar.
Tópicos deste artigo
- 1 - União de conjuntos
- 2 - Intersecção de conjuntos
- 3 - Diferença de conjuntos
- 4 - Conjuntos complementares
- 5 - Exercícios resolvidos
União de conjuntos
A união entre dois ou mais conjuntos será um novo conjunto constituído por elementos que pertencem a, pelo menos, um dos conjuntos em questão. Formalmente o conjunto união é dado por:
![]()
Sejam A e B dois conjuntos, a união entre eles é formada por elementos que pertencem ao conjunto A ou ao conjunto B.
Em outras palavras, basta unir os elementos de A com os de B.

Exemplo:
a) Considere os conjuntos A = {0, 2, 4, 6, 8, 10} e B = {1, 3, 5, 7, 9, 11}:
A U B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
b) A = {x | x é um número par natural} e B {y | y é um número ímpar natural}
A união de todos os pares naturais e todos os ímpares naturais resulta em todo o conjunto dos números naturais, logo, temos que:
![]()
Intersecção de conjuntos
A intersecção entre dois ou mais conjuntos também será um novo conjunto formado por elementos que pertencem, ao mesmo tempo, a todos os conjuntos envolvidos. Formalmente temos:
![]()
Sejam A e B dois conjuntos, a intersecção entre eles é formada por elementos que pertencem ao conjunto A e ao conjunto B. Desse modo, devemos considerar somente os elementos que estão em ambos os conjuntos.
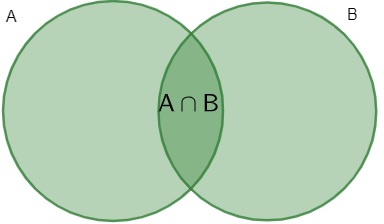
Exemplo
a) Considere os conjuntos A = {1, 2, 3, 4, 5, 6}, B = {0, 2, 4, 6, 8, 10} e C = {0, –1, –2, –3}
A ∩ B = {2, 4, 6}
A ∩ C = { }
B ∩ C = {0}
O conjunto que não possui nenhum elemento é chamado de conjunto vazio e pode ser represento de duas formas.
![]()
Leia também: Definição de conjunto
Diferença de conjuntos
A diferença entre dois conjuntos, A e B, é dada pelos elementos que pertencem a A e não pertencem a B.
![]()
No diagrama de Venn-Euler, a diferença entre os conjuntos A e B é:
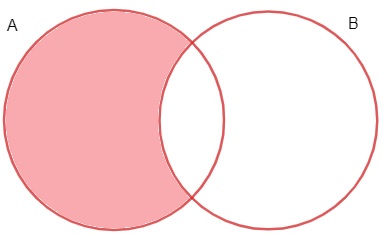
Exemplo
Considere os conjuntos A = {0, 1, 2, 3, 4, 5, 6, 7}, B = {0, 1, 2, 3, 4, 6, 7} e C = { }. Vamos determinar as seguintes diferenças.
A – B = {5}
A – C = {0, 1, 2, 3, 4, 5, 6, 7}
C – A = { }
Observe que, no conjunto A – B, tomamos inicialmente o conjunto A e “tiramos” os elementos do conjunto B. No conjunto A – C, tomamos o A e “tiramos” o vazio, ou seja, nenhum elemento. Por último, em C – A, tomamos o conjunto vazio e “tiramos” os elementos de A, que, por sua vez, já não estavam lá.
Leia também: Notações importantes sobre conjuntos
Conjuntos complementares
Considere os conjuntos A e B, em que o conjunto A está contido no conjunto B, isto é, todo elemento de A também é elemento de B. A diferença entre os conjuntos, B – A, é chamada de complementar de A em relação a B. Em outras palavras, o complementar é formado por todo elemento que não pertence ao conjunto A em relação ao conjunto B, em que ele está contido.
![]()
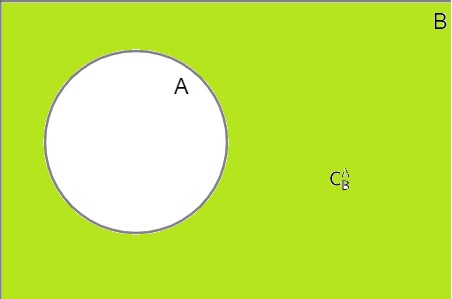
Exemplo
Considere os conjuntos A = {0, 1, 2, 3, 4, 5} e B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
O complementar de A em relação a B é:
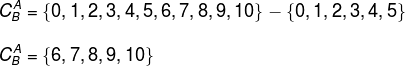
Exercícios resolvidos
Questão 1 – Considere os conjuntos A = {a, b, c, d, e, f} e B ={d, e, f, g, h, i}. Determine (A – B) U (B – A).
Solução
Inicialmente determinaremos os conjuntos A – B e B – A e, em seguida, realizaremos a união entre eles.
A – B = {a, b, c, d, e, f} – {d, e, f, g, h, i}
A – B = {a, b, c}
B – A = {d, e, f, g, h, i} – {a, b, c, d, e, f}
B – A = {g, h, i}
Logo, (A – B) U (B – A) é:
{a, b, c} U {g, h, i}
{a, b, c, g, h, i}
Questão 2 – (Vunesp) Suponhamos que A U B = {a, b, c, d, e, f, g, h}, A ∩ B = {d, e} e A – B = {a, b, c}, então:
a) B = {f, g, h}
b) B = {d, e, f, g, h}
c) B = { }
d) B = {d, e}
e) B = {a, b, c, d, e}
Solução
Alternativa b.
Dispondo os elementos no diagrama de Venn-Euler, segundo o enunciado, temos:
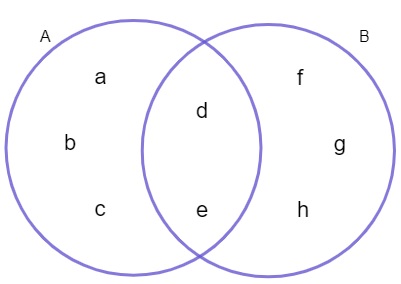
Portanto, o conjunto B = {d, e, f, g, h}.
Por Robson Luiz
Professor de Matemática

