A divisão com vírgula acontece quando há casa decimais no divisor ou no dividendo, ou então em ambos os números. Para calcular a divisão quando o número tem vírgula, realizamos alguns ajustes na parte decimal. Após igualar a quantidade de algarismos depois da vírgula, podemos ignorar a vírgula e realizar a divisão normalmente, assim como é realizada entre dois números inteiros.
Leia também: Como resolver operações com números decimais
Tópicos deste artigo
- 1 - Resumo sobre divisão com vírgula
- 2 - Videoaula sobre divisão com números decimais (divisão com vírgula)
- 3 - Quais as regras para fazer a divisão com vírgula?
- 4 - Exercícios resolvidos sobre divisão com vírgula
Resumo sobre divisão com vírgula
- A divisão com vírgula é uma divisão que envolve números decimais.
- Podemos ter um número com vírgula no divisor, no dividendo ou em ambos.
- Para calcular a divisão com vírgula, é necessário igualar a quantidade de algarismos na parte decimal, depois retirar a vírgula e dividir normalmente.
Videoaula sobre divisão com números decimais (divisão com vírgula)
Quais as regras para fazer a divisão com vírgula?
→ Regras da divisão com vírgula no quociente (divisão não exata)
A divisão possui vírgula no quociente quando ela não é exata, ou seja, quando o resto é diferente de zero. Quando a divisão não é exata, podemos encontrar um quociente decimal, ou seja, um número com vírgula no quociente. Quando a divisão possui resto diferente de zero, para calcular a divisão, adicionamos a vírgula no quociente e acrescenta-se zero no resto, continuando o processo de divisão normalmente.
Exemplo:
| 17 : 4 |
Queremos calcular 17 divido por 4. Sabemos que o número que multiplicado por 4 que chega mais próximo ao 4 é o 4, pois 4 vezes 4 é igual a 16. Logo, temos que:
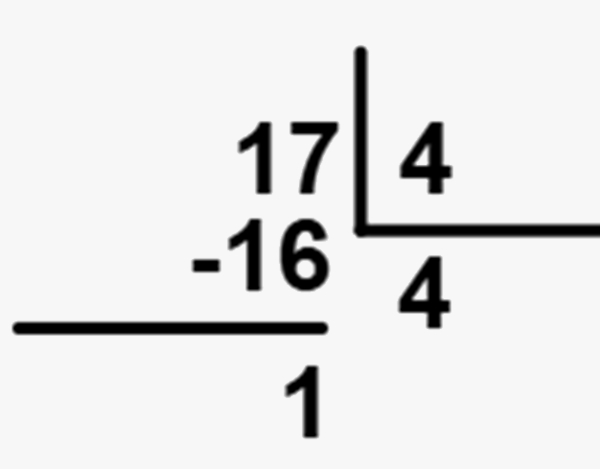
Note que o resto é 1, logo acrescentaremos a vírgula no quociente e multiplicaremos o resto por 10, ou seja, acrescentaremos um 0 atrás do 1:
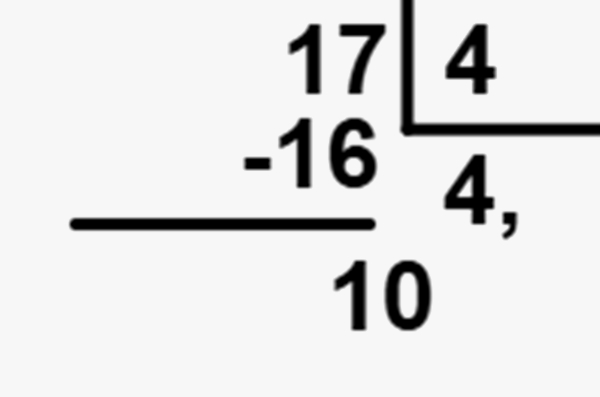
Então encontraremos que número vezes 4 chega mais próximo de 10; no caso, é o 2.
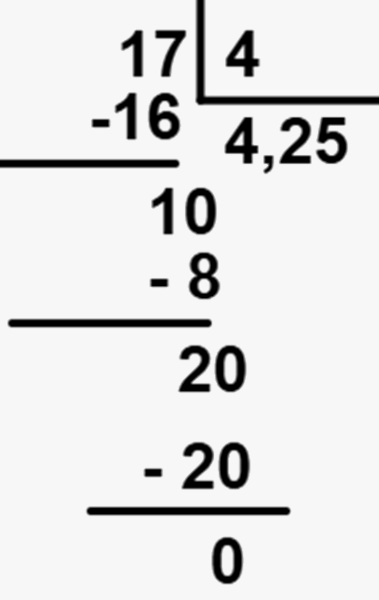
Como se trata da parte decimal, descemos um zero para o resto, logo o resto será 20. E encontraremos o número que multiplicado por 4 chega mais próximo de 20, que no caso é o 5, pois 5 vezes 4 é igual a 20.
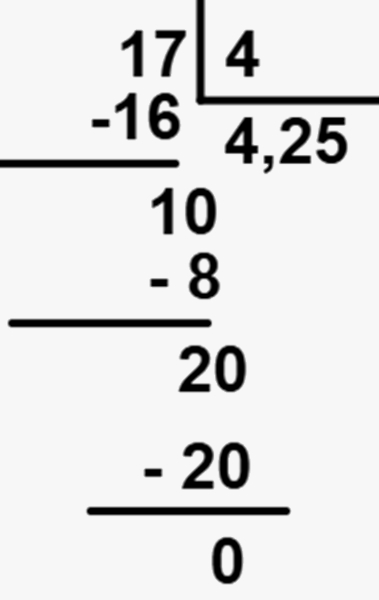
Então 17 : 4 = 4,25
→ Regras da divisão com vírgula no divisor e no dividendo
Para realizar esse tipo de divisão, é necessário que o dividendo e o divisor tenham a mesma quantidade de casas decimais após a vírgula. Isso permite que a vírgula seja eliminada de forma prática. Para alcançar esse objetivo, multiplicamos ambos os valores por uma potência de 10 apropriada, convertendo-os em números inteiros.
Por exemplo, se tanto o dividendo quanto o divisor tiverem um algarismo após a vírgula, multiplicamos ambos por 10, eliminando assim a vírgula e transformando os números em inteiros. Esse procedimento facilita os cálculos, pois trabalhar com números inteiros é mais simples do que com decimais, e o valor relativo entre os números permanece o mesmo. Se houver dois algarismos após a vírgula, multiplicamos por 100, ajustando conforme o número de casas decimais necessário para garantir a exatidão do resultado final.
Exemplos:
a) Calcule a divisão entre 4,5 e 0,9.
Resolução:
Note que tanto 4,5 quanto 0,9 possuem somente uma casa decimal. Nesse caso, multiplicaremos ambos por 10. Desse modo encontraremos os números 45 e 9, então basta calcular a divisão:
4,5 : 0,9 = 45 : 9 = 5
b) Calcule a divisão 8,5 : 1,25.
Note, nesse caso, que há um número depois da vírgula no divisor e dois números depois da vírgula no dividendo. Então, para igualar a quantidade de números depois da vírgula multiplicaremos ambos por 100; logo, temos que:
8,5 : 1,25 = 850 : 125
Agora basta calcular a divisão normalmente:
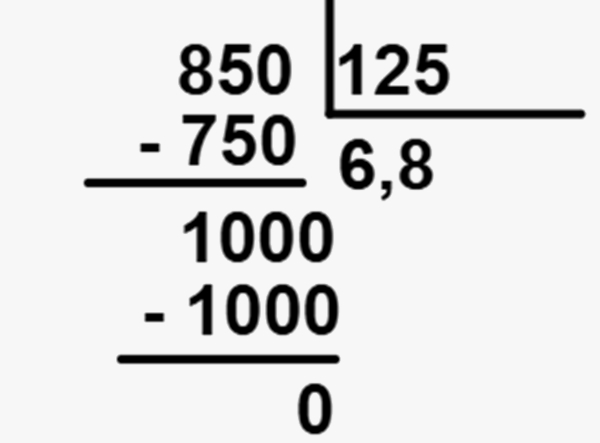
→ Regras da divisão com vírgula no divisor
Quando o divisor é um número decimal, a divisão precisa ser ajustada para facilitar o cálculo. Para isso, multiplicamos o divisor e o dividendo pelo mesmo fator de 10, de modo que o divisor se torne um número inteiro. O número de zeros a ser adicionado ao dividendo depende da quantidade de casas decimais presentes no divisor. Esse ajuste torna a operação mais simples e direta.
Exemplo:
Calcule:
| 18 : 0,9 |
Note que o divisor possui um número depois da vírgula, então podemos reescrever a divisão da seguinte maneira:
18,0 : 0,9 = 180 : 9
Agora basta calcular a divisão:
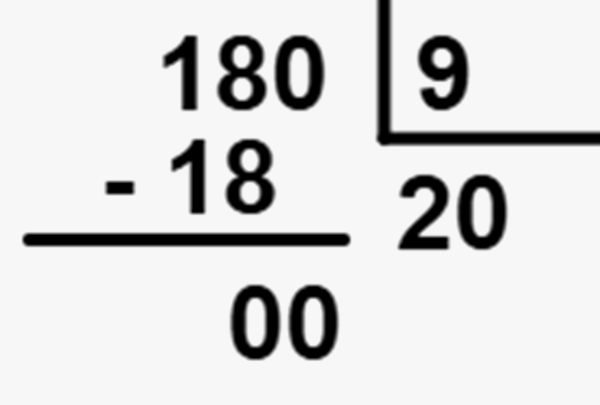
→ Regras da divisão com vírgula no dividendo
Para realizar a divisão de números decimais, é preciso ajustar o divisor para que ele tenha o mesmo número de casas decimais que o dividendo. Dessa forma, as vírgulas em ambos os números podem ser eliminadas, facilitando o cálculo.
Exemplo:
Calcule a divisão
| 13,5 : 9 |
Então temos que:
13,5 : 9 = 13,5 : 9,0 = 135 : 90
Calculando a divisão temos que:
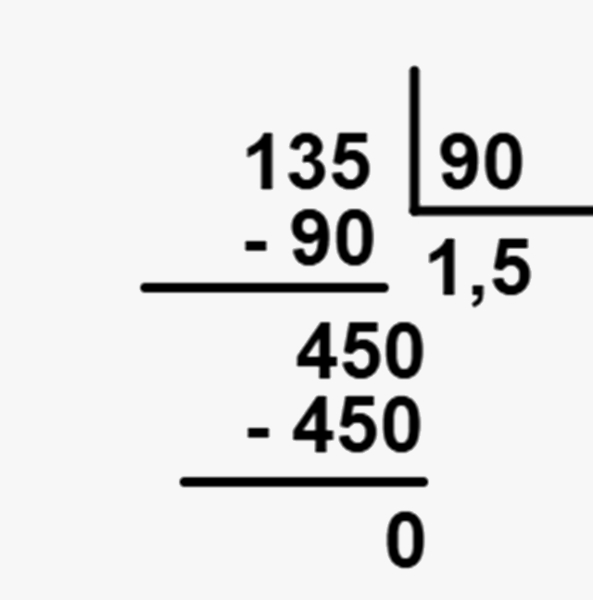
→ Regras da divisão com dividendo menor que o divisor
Quando o dividendo é menor que o divisor, devemos adicionar um zero e uma vírgula ao quociente, além de acrescentar um zero ao dividendo antes de iniciar a operação. Esse procedimento resulta em um quociente decimal que será inferior a 1.
Exemplo:
Calcule a divisão
| 2 : 5 |
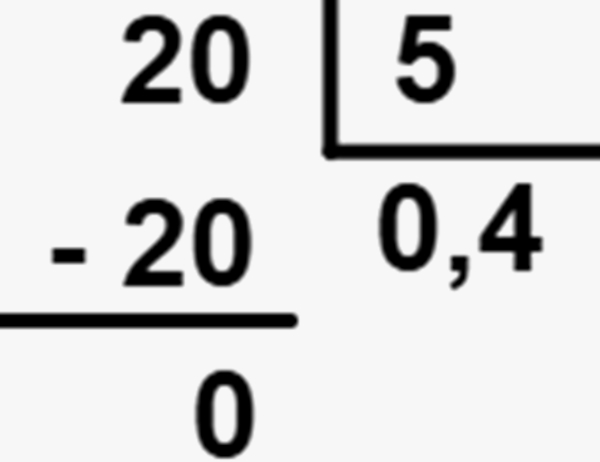
Então acrescentaremos um 0 no dividindo; logo, ele será igual a 20, e o quociente iniciará com 0.
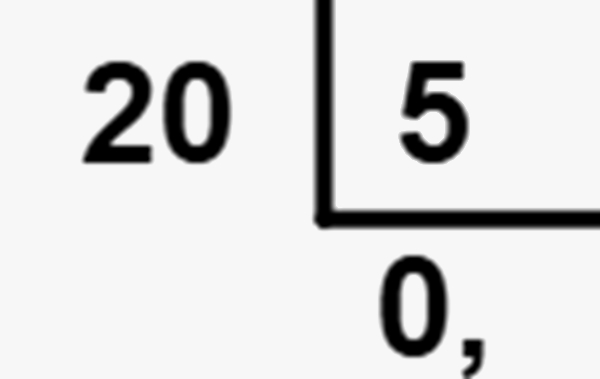
Agora encontraremos qual número multiplicado por 5 é igual a 20 – no caso, 4.
Saiba mais: O que são múltiplos e divisores de um número?
Exercícios resolvidos sobre divisão com vírgula
Questão 1
Após realizar a compra do supermercado, Natália recebeu um troco de R$ 20,50 e decidiu dividir igualmente esse troco entre suas filhas Fernanda e Francisca. O valor que cada uma delas recebeu é de:
A) 10,25
B) 10,20
C) 12,25
D) 12,50
E) 12,75
Resolução:
Alternativa A
Calculando a divisão, temos que:
20,50 : 2 = 20,5 : 2,0 = 205 : 20
Calculando a divisão, temos que:
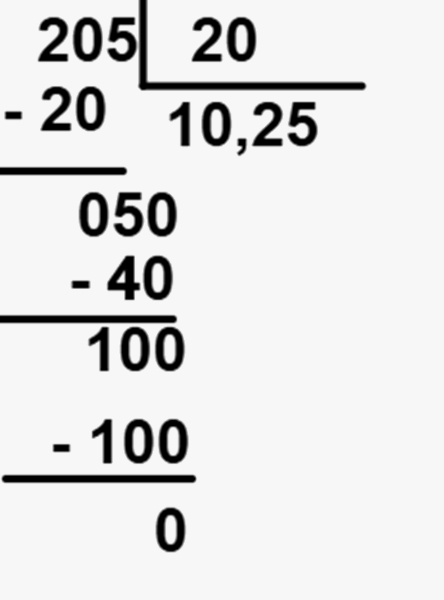
Cada uma delas receberá R$ 10,25.
Questão 2
Um metro e meio de corda será dividido em vários pedaços contendo 0,3 metro cada, então a quantidade de cordas de 0,3 metro que teremos é:
a) 3
b) 4
c) 5
d) 6
e) 7
Resolução:
Alternativa C
Queremos calcular 1,5 : 0,3 , mas note que todos possuem a mesma quantidade de números na parte decimal, então 1,5 : 0,3 = 15 : 3 = 5. Conclui-se que teremos 5 cordas com 0,3 metro cada.
Fonte
Caraça, Bento de Jesus. Conceitos Fundamentais da Matemática. Ed. Gradiva. Coleção Ciência Aberta.2005.

