O que é potenciação?

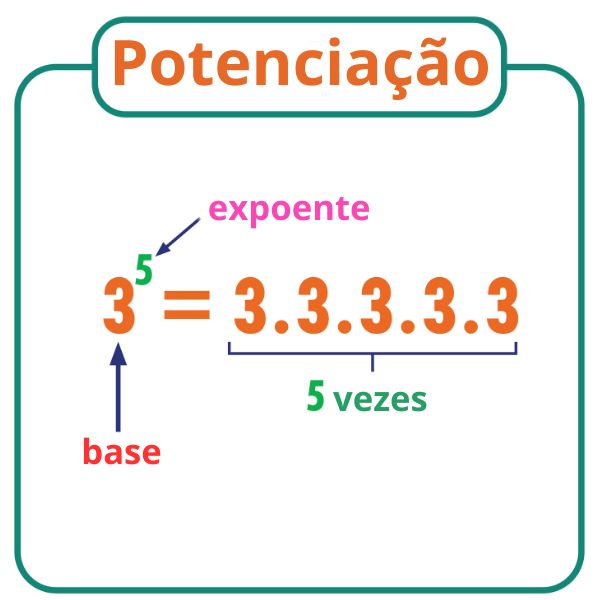
A potenciação é uma operação matemática. Utilizamos a potenciação para indicar multiplicações consecutivas de um mesmo fator. Por exemplo, 3⁵  representa 5 multiplicações do número 3, o que resulta em 243. Dizemos que 3 é a base, 5 é o expoente e 243 é a potência.

Neste texto descobriremos como calcular qualquer potência e como utilizar as principais propriedades de potenciação para simplificar cálculos. Além disso, conheceremos alguns casos particulares da potenciação, que exigem atenção especial.

Leia também: Radiciação — a operação inversa à potenciação

Tópicos deste artigo

• 1 - Videoaula sobre potenciação
• 2 - Propriedades da potenciação 
  • Multiplicação de potências de mesma base
  • Divisão de potências de mesma base
  • Potência de potência
  • Potência de produto
  • Potência de quociente
• 3 - Como calcular as potências?
• 4 - Casos particulares de potenciação
  • Expoente unitário
  • Expoente zero
  • Expoente negativo
  • Expoente fracionário
• 5 - Como se lê uma potência?
• 6 - Diferenças entre radiciação e potenciação
• 7 - Exercícios resolvidos sobre potenciação

Videoaula sobre potenciação

Propriedades da potenciação 

Vejamos cinco das principais propriedades de potenciação.

• Multiplicação de potências de mesma base

Seja x um número real, assim x^m e xⁿ são duas potências de mesma base. Calcular o produto $x^m.x^n$ e calcular a potência $x^{m+n}$ levam ao mesmo resultado, ou seja:

$x^m.x^n=x^{m+n}\ $ 

Exemplo:

Observe que:

$2^3=8$

$2^4=16$

$2^3.2^4=8.16=128$

Além disso:

$2^{3+4}=2^7=128$

Dessa forma, $2^3.2^4$ e $2^{3+4}$ resultam em 128.

• Divisão de potências de mesma base

Seja x um número real, assim x^m e xⁿ são duas potências de mesma base. Calcular o quociente $\frac{x^m}{x^n}$ e calcular a potência x^m-n levam ao mesmo resultado, ou seja:

$\frac{x^m}{x^n}=x^{m-n}$

Exemplo:

Observe que:

$3^5=243$

$3^2=9$

$\frac{3^5}{3^2}=\frac{243}{9}=27$

Além disso:

$3^{5-2}=3^3=27$

Dessa forma, $\frac{3^5}{3^2}$ e $3^{5-2}$ resultam em 27.

• Potência de potência

Seja x um número real, assim $x^m$ é uma potência e $\left(x^m\right)^n$ é uma potência de potência.

Calcular primeiro a potência $x^m$ e elevar ao expoente n  e calcular a potência xm.n  levam ao mesmo resultado, ou seja:

$\left(x^m\right)^n=x^{m.n}$

Exemplo:

Observe que:

$\left(4^2\right)^3={16}^3=4096$

Além disso:

$4^{2.3}=4^6=4096$

Dessa forma, $\left(4^2\right)^3$e $4^{2.3}$ resultam em 4096.

Cuidado: Existe diferença entre $\left(x^m\right)^n$ e $x^{m^n}$. No primeiro caso, a potência $x^m$ possui n  como expoente. No segundo caso, n é expoente apenas de m . Compare:

$\left(2^2\right)^3=4^3=64$

$2^{2^3}=2^8=256$

• Potência de produto

Sejam x e y números reais, assim, $\left(x.y\right)^n$ é a potência de um produto.

Calcular primeiro o produto $x.y$ e elevar ao expoente n  e calcular o produto entre as potências $x^n$ e $y^n$ levam ao mesmo resultado, ou seja:

$\left(x.y\right)^n=x^n.y^n$

Exemplo:

Observe que:

$\left(5.2\right)^3={10}^3=1000$

Além disso:

$5^3.2^3=125.8=1000$

Dessa forma, $\left(5.2\right)^3$ e $5^3.2^3$ resultam em 1000.

• Potência de quociente

Sejam x e y números reais, assim $\left(\frac{x}{y}\right)^n$é a potência de um quociente.

Calcular primeiro o quociente $\frac{x}{y}$e elevar ao expoente n  e calcular o quociente entre as potências $x^n$ e $y^n$ levam ao mesmo resultado, ou seja:

$\left(\frac{x}{y}\right)^n=\frac{x^n}{y^n}$

Exemplo:

Observe que:

$\left(\frac{6}{3}\right)^4=2^4=16$

Além disso:

$\frac{6^4}{3^4}=\frac{1296}{81}=16$

Dessa forma, $\left(\frac{6}{3}\right)^4$ e $\frac{6^4}{3^4}$ resultam em 16.

Leia também: Potências de base — tipo de potência muito comum em cálculos na Física

Como calcular as potências?

Para calcular uma potência, devemos resolver multiplicações sequenciais entre um mesmo fator. Lembre-se que a base indica o número que será multiplicado e o expoente indica quantas vezes devemos multiplicar esse número.

Exemplos:

$(-{4)}^3=\left(-4\right).\left(-4\right).\left(-4\right)=-64$

$2^9=2.2.2.2.2.2.2.2.2=512$

Casos particulares de potenciação

• Expoente unitário

Seja x um número real, então x¹ indica uma multiplicação de x, portanto, uma potência com expoente 1 resulta no valor da base.

Dessa forma:

$x^1=x$

Exemplos:

$\left(-5\right)^1=-5$

${23.567}^1=23.567$

• Expoente zero

Seja x um número real, então:

$x^0=1$

Parece estranho ou sem sentido? Vamos analisar um exemplo com x=3 .

Exemplo:

Observe a imagem abaixo, que apresenta diferentes expoentes para a base 3. Pela definição de potenciação (uma multiplicação de fatores iguais), se a cada linha aumentamos 1 no expoente, devemos incluir um fator 3 multiplicando. Portanto, para que o padrão seja mantido, $3^1$  deve ser o triplo de $3^0$, logo, $3^0=1$.

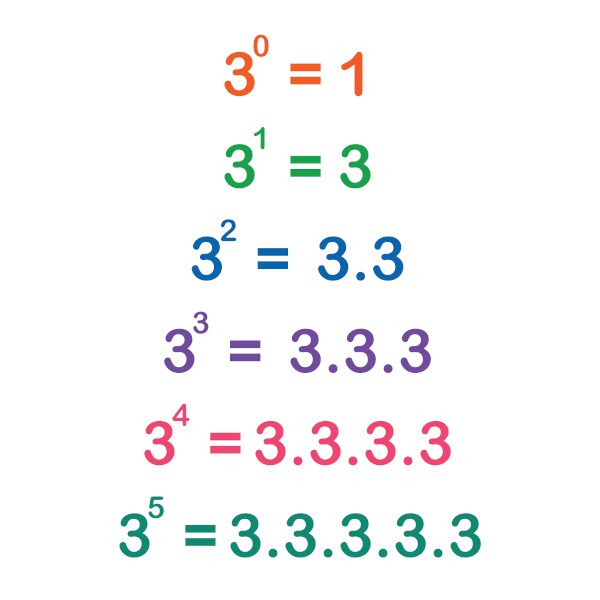
• Expoente negativo

Seja x um número real, e estendendo a análise do item anterior, podemos concluir que $x^{-1}$ é o inverso multiplicativo de x , ou seja:

$x^{-1}=\frac{1}{x}$

Exemplos:

$2^{-1}=\frac{1}{2}$

${15}^{-1}=\frac{1}{15}$

• Expoente fracionário

Seja x um número real, então xmn  indica uma raiz de índice n  e radicando xm , ou seja:

$x^\frac{m}{n}\ =\ \sqrt[n]{x^m}$

Exemplos:

$2^\frac{1}{3}=\sqrt[3]{2^1}$

$4^\frac{3}{2}=\sqrt[2]{4^3}$

Como se lê uma potência?

Se o expoente for 2, lemos que a base está elevada ao quadrado ou à potência 2 ou à segunda potência.

Se o expoente for 3, lemos que a base está elevada ao cubo ou à potência 3 ou à terceira potência.

Para expoente n qualquer, lemos que a base está elevada à enésima potência.

Exemplos:

• 3²  — três ao quadrado; três elevado ao quadrado; três elevado à segunda potência.
• 5³  — cinco ao cubo; cinco elevado ao cubo; cinco elevado à terceira potência.
• 7⁹  — sete elevado à nona potência.

Diferenças entre radiciação e potenciação

A radiciação é a operação inversa da potenciação. Enquanto na potenciação partimos da multiplicação dos fatores para obter a potência, na radiciação partimos da potência (ou seja, do resultado da potenciação) para encontrar os fatores.

Assim, dizer que $\sqrt[n]{k\ }=x$ significa dizer que $x^n=k$. Por exemplo, $\sqrt[3]{8}\ =2$,  pois $2^3=8.$

Leia também: Como resolver expressões numéricas

Exercícios resolvidos sobre potenciação

Questão 1

(Enem PPL 2021) A imagem representa uma calculadora científica com duas teclas destacadas. A tecla A eleva ao quadrado o número que está no visor da calculadora, e a tecla B extrai a raiz cúbica do número apresentado no visor:

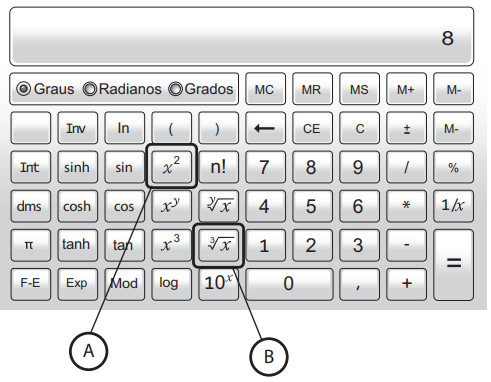
Uma pessoa digitou o número 8 na calculadora e em seguida apertou três vezes a tecla A e depois uma vez a tecla B.

A expressão que representa corretamente o cálculo efetuado na calculadora é:

a) $\sqrt[2]{8^{3+3+3}}$

b) $\sqrt[3]{8^{2\times2\times2}}$

c) $\sqrt[2]{8^3+8^3+8^3}$

d) $\sqrt[3]{8^2+8^2+8^2}$

e) $\sqrt[3]{8^2\times8^2\times8^2}$

Resolução:

Apertar três vezes a tecla A significa calcular $\left(\left(8^2\right)^2\right)^2$. Perceba que essa expressão envolve potência de potência. Assim, aplicando a propriedade:

$\left(\left(8^2\right)^2\right)^2=8^{2\times2\times2}$

Apertar uma vez a tecla B significa calcular $\sqrt[3]{8^{2\times2\times2}}$ .

Alternativa B

Questão 2

(UFRGS) Por qual potência de 10 deve ser multiplicado o número ${10}^{-3}\ \times{10}^{-3}\times{10}^{-3}\times{10}^{-3}$ para que esse produto seja igual a 10?

a) 10⁹

b) 10¹⁰

c) 10¹¹

d) 10¹²

e) 10¹³

Resolução:

Como o produto possui potências de mesma base, podemos aplicar a propriedade:

${10}^{-3}\times{10}^{-3}\times{10}^{-3}\times{10}^{-3}={10}^{\left(-3\right)+\left(-3\right)+\left(-3\right)+\left(-3\right)}={10}^{-12}$

Perceba que:

${10}^{-12}\times{\mathbf{10}}^{\mathbf{13}}={10}^{-12+13}={10}^1=10$

Alternativa E

Por Maria Luiza Alves Rizzo
Professora de Matemática