Balanceamento químico

Balanceamento químico é o processo de ajustar os coeficientes de uma equação química para garantir que o número de átomos de cada elemento seja o mesmo em ambos os lados da equação. Esse princípio é baseado na lei de conservação das massas, formulada por Antoine Lavoisier, que estabelece que a massa não pode ser criada nem destruída em uma reação química, apenas transformada. Portanto, ao escrever uma equação química, é essencial que a quantidade de cada átomo presente nos reagentes seja exatamente igual à quantidade dos mesmos átomos nos produtos.

O balanceamento químico pode ser feito por diferentes métodos, como o método das tentativas (ou método indireto), o método algébrico, e o método redox (redução-oxidação). Cada um desses métodos tem vantagens e níveis de complexidade diferentes, dependendo da reação a ser balanceada.

O balanceamento é fundamental para entender as relações quantitativas em uma reação, permitindo calcular a quantidade exata de reagentes necessários para produzir certa quantidade de produtos. Além disso, ele é essencial para garantir a precisão em experimentos de laboratório e processos industriais que envolvem reações químicas.

Leia também: Como fazer cálculos estequiométricos

Tópicos deste artigo

• 1 - Resumo sobre balanceamento químico
• 2 - Videoaula sobre balanceamento químico
• 3 - Como fazer o balanceamento químico?
• 4 - Métodos de balanceamento químico
  • → Método das tentativas ou indireto
  • → Método algébrico
  • → Método redox
• 5 - Regras para o balanceamento químico
• 6 - Função do balanceamento químico
• 7 - Macetes para fazer balanceamento químico
• 8 - Exercícios resolvidos sobre balanceamento químico

Resumo sobre balanceamento químico

• O balanceamento químico envolve a adição de coeficientes estequiométricos às substâncias envolvidas em uma reação química.
• O balanceamento de equações químicas pode ser feito pelo método das tentativas (ou método indireto); método algébrico; ou método redox.
• O balanceamento deve ser feito conservando a quantidade de átomos de cada elemento.
• É fundamental para realizar cálculos estequiométricos, prever a eficiência das reações e realizar experimentos controlados.
• A regra do Macho é um macete muito útil para lembrar a sequência dos elementos a serem balanceados (Metais; Ametais; Carbono; Hidrogênio; Oxigênio).
• Exercícios sobre balanceamento químico.

Videoaula sobre balanceamento químico

Como fazer o balanceamento químico?

O balanceamento químico envolve a adição de coeficientes estequiométricos às substâncias envolvidas em uma reação química. Esses coeficientes são números colocados na frente das fórmulas dos compostos para garantir que o número de átomos de cada elemento seja o mesmo nos dois lados da equação.

Vamos usar a reação abaixo como exemplo para ilustrar o processo de balanceamento:

Al₂O₃​ + HCl → AlCl₃ + H₂O

• Passo 1: Identificar os átomos presentes. No lado dos reagentes, temos dois átomos de alumínio (Al), três átomos de oxigênio (O), um átomo de hidrogênio (H) e um átomo de cloro (Cl). Do lado dos produtos, temos um átomo de alumínio, três átomos de cloro, dois átomos de hidrogênio e um átomo de oxigênio. Nosso objetivo é igualar o número de átomos de cada elemento em ambos os lados da equação.

• Passo 2: Começar pelo elemento que aparece em menos compostos. O alumínio (Al) está presente em um composto em cada lado da equação. No reagente, temos Al₂​, ou seja, dois átomos de alumínio. No produto, há apenas um átomo de alumínio em AlCl₃. Para equilibrar isso, multiplicamos AlCl₃​ por 2:

Al₂O₃​ + HCl → 2 AlCl₃ + H₂O

Agora temos dois átomos de alumínio em ambos os lados.

• Passo 3: Balancear o cloro. No lado dos produtos, temos seis átomos de cloro, já que 2 AlCl₃ contém seis átomos de cloro. Para equilibrar isso, multiplicamos HCl por 6 no lado dos reagentes:

Al₂O₃​ + 6 HCl → 2 AlCl₃ + H₂O

Agora temos seis átomos de cloro em ambos os lados.

• Passo 4: Balancear o hidrogênio. No lado dos produtos, temos seis átomos de hidrogênio (6 HCl), então, para equilibrar isso, multiplicamos o H₂​O por 3 no lado dos produtos:

Al₂O₃​ + 6 HCl → 2 AlCl₃ + 3 H₂O

Agora, temos seis átomos de hidrogênio em ambos os lados.

Passo 5: Verificar e balancear o número de oxigênio. Como há três átomos de oxigênio no lado dos reagentes (Al₂O₃​) e três átomos de oxigênio no lado dos produtos (3 H₂O), o oxigênio já está balanceado.

A equação final balanceada é:

Al₂Cl₃​ + 6 HCl → 2 AlCl₃ + 3 H₂O

Após o balanceamento, é realizada uma contagem do número de átomos de cada elemento, comparando ambos os lados da equação. Como o balanceamento segue a lei de conservação das massas, o número de átomos de cada elemento no lado dos reagentes deve ser igual ao número de átomos no lado dos produtos.

Veja também: Quais são os tipos de reações orgânicas existentes?

Métodos de balanceamento químico

O balanceamento de equações químicas pode ser feito por diferentes métodos, cada um com características específicas. Os três principais métodos são:

• Método das tentativas (ou método indireto): um dos mais simples e amplamente utilizados, especialmente em reações orgânicas e inorgânicas básicas.

• Método algébrico: usa variáveis para resolver sistemas de equações, e é muito utilizado em reações mais complexas.

• Método redox: específico para reações de oxirredução, em que é necessário balancear a variação de números de oxidação.

→ Método das tentativas ou indireto

O método das tentativas consiste em balancear a equação química por meio de tentativas sucessivas. Para isso, aplicamos coeficientes aos compostos, ajustando-os conforme necessário até que o número de átomos de cada elemento seja o mesmo nos dois lados da equação. Esse método é bastante intuitivo, sendo muito usado em situações nas quais a equação não é muito complexa.

Vamos exemplificar com a seguinte reação:

C₂H₆O + O₂ ​→ CO₂ ​+ H₂​O

• Passo 1: Começar balanceando o carbono (C). No reagente, temos dois átomos de carbono (C₂H₆O), enquanto, no produto, cada molécula de CO₂​ contém um átomo de carbono. Para equilibrar o carbono, multiplicamos CO₂​ por 2:

C₂H₆O + O₂ ​→ 2 CO₂ ​+ H₂​O

• Passo 2: Balancear o hidrogênio. No reagente, temos seis átomos de hidrogênio (C₂H₆O), enquanto, no produto, cada molécula de H₂O contém dois átomos de hidrogênio. Para equilibrar o hidrogênio, multiplicamos H₂O por 3:

C₂H₆O + O₂ ​→ 2 CO₂ ​+ 3 H₂​O

• Passo 3: Balancear o oxigênio. No lado dos produtos, temos quatro átomos de oxigênio no CO₂​ (2 × 2) e três átomos de oxigênio no H₂O, totalizando sete átomos de oxigênio. No lado dos reagentes, temos um átomo de oxigênio em C₂H₆O. Precisamos de mais seis átomos de oxigênio para equilibrar a equação, então multiplicamos O₂ por 3:

C₂H₆O + 3 O₂ ​→ 2 CO₂ ​+ 3 H₂​O

Fazendo 3 O₂, temos um total de seis oxigênios, que, somados a mais um, no C₂H₆O, totalizam sete átomos de oxigênio no lado dos reagentes. Assim, a equação final balanceada é:

C₂H₆O + 3 O₂ ​→ 2 CO₂ ​+ 3 H₂​O

→ Método algébrico

O método algébrico envolve a resolução de um sistema de equações lineares, atribuindo coeficientes variáveis para cada composto na equação. Vamos usar a reação entre o dióxido de enxofre (SO₂) e oxigênio (O₂​) para formar trióxido de enxofre (SO₃):

SO₂ + O₂ → SO₃

• Passo 1: Atribuir variáveis aos coeficientes:

a SO₂ + b O₂ → c SO₃

• Passo 2: Encontra-se o número de átomos de cada elemento nos dois membros da equação e, em seguida, escreve-se as equações para o balanceamento dos átomos de cada elemento, em que a seta (→) será representada pela igualdade (=). Veja, seguir, o procedimento:

a) Montando a equação para o enxofre (S): Analisando a equação química, observa-se que existem apenas um átomo de enxofre no SO₂, coeficiente a, e um átomo de enxofre no SO₃, coeficiente c. Assim, temos 1.a = 1.c, ou seja:

a = c

b) Montando a equação para o oxigênio (O): Analisando a equação química, observa-se que existem dois átomos de oxigênio no SO₂, coeficiente a, dois átomos de oxigênio no O₂, coeficiente b, e três átomos de enxofre no SO₃, coeficiente c. Assim, temos 2.a + 2.b = 3.c, ou seja:

2a + 2b = 3c

• Passo 3: Resolver o sistema de equações:
  • Equação 1: a = c   
  • Equação 2: 2a + 2b = 3c  

Como a = c, substituímos c por a na equação do oxigênio, logo:

2a + 2b = 3a

Simplificando, temos 2b = 3a ⎼ 2a, logo:

2b = a

Portanto:

\(b = \frac{a}{2} b = \frac{a}{2} b = \frac{a}{2} \)

Assim, podemos escolher a = 2 para evitar frações, resultando em b = 1. Como a = c, logo, c = 2.

Agora é só substituir as variáveis pelos valores para ter os coeficientes e a equação balanceada:

2 SO₂ + O₂ → 2 SO₃

→ Método redox

O método de balanceamento por oxirredução (ou método redox) é uma técnica usada para balancear equações químicas em que há transferência de elétrons entre os reagentes, ou seja, em que ocorre uma mudança nos números de oxidação (NOX) dos elementos envolvidos. O NOX indica o número de elétrons que um átomo ganha ou perde durante uma reação.

No método redox, a ideia é ajustar os coeficientes da equação para garantir que o número de elétrons perdidos em um processo de oxidação seja igual ao número de elétrons ganhos em um processo de redução.

Vamos aplicar esse método ao balanceamento da reação entre permanganato de potássio (KMnO₄) e ácido clorídrico (HCl):

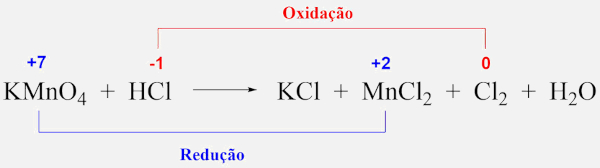
KMnO₄ + HCl→ KCl + MnCl₂ ​+ Cl₂ ​+ H₂​O

• Passo 1: Identificar os elementos que sofrem oxidação e redução.

A primeira etapa é identificar quais elementos estão mudando de NOX durante a reação.

• • O manganês (Mn) no KMnO₄​ tem NOX +7 (no íon permanganato, MnO₄⁻).
  • No MnCl₂​, o manganês tem NOX +2.
  • O cloro (Cl) no HCl tem NOX -1, enquanto, no Cl₂​ (gás cloro), o NOX é 0.

Na reação, o manganês (Mn) está sendo reduzido de +7 para +2, e o cloro (Cl) está sendo oxidado de -1 para 0.

• Passo 2: Determinar a variação total do NOX

A variação total do NOX (∆) é o produto da variação desse NOX (v) pelo índice da entidade que sofre oxidação ou redução (i):

∆ = v . i

Quando a entidade química apresenta índices diferentes na equação, o valor do maior índice deve ser utilizado.

Agora, devemos calcular a variação total do NOX (∆) para os elementos que estão sendo oxidados e reduzidos.

• Variação do manganês (∆Mn): De +7 para +2, há uma variação de cinco elétrons ganhos, e, como o índice do manganês é 1, temos:

∆ = 5 . 1 = 5

• Variação do cloro (∆Cl): De -1 para 0, há uma variação de um elétron perdido, e, como o maior índice para o átomo de cloro é 2, no Cl₂, temos:

∆ = 1 . 2 = 2

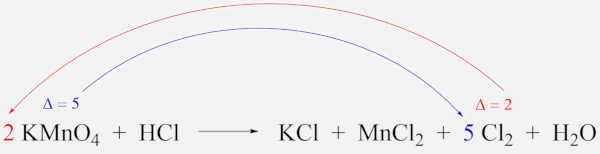
• Passo 3: Inverter os valores da variação total (∆) e utilizá-los como coeficientes.

Em uma reação de oxirredução, o número total de elétrons perdidos na oxidação é igual ao número de elétrons ganhos na redução. Assim, temos:

• Passo 4: Balancear os átomos restantes pelo método de tentativas.

Agora que os elétrons estão balanceados, balanceamos o restante dos átomos:

2 KMnO₄ + HCl→ KCl + MnCl₂ ​+ 5 Cl₂ ​+ H₂​O

Existem dois átomos de potássio e dois átomos de manganês no lado dos reagentes​. Então é preciso adicionar o coeficiente 2 para o KCl e 2 para o MnCl₂, no lado dos produtos, a fim de igualar a quantidade de átomos de potássio e de manganês em ambos os lados da equação. Assim, temos:

2 KMnO₄ + HCl→ 2 KCl + 2 MnCl₂ ​+ 5 Cl₂ ​+ H₂​O

Agora, existem 16 átomos de cloro no lado dos produtos​. Então, é preciso adicionar o coeficiente 16 para o HCl, no lado dos reagentes, a fim de igualar a quantidade de átomos de cloro em ambos os lados da equação. Assim, temos:

2 KMnO₄ + 16 HCl→ 2 KCl + 2 MnCl₂ ​+ 5 Cl₂ ​+ H₂​O

Agora, existem 16 átomos de hidrogênio no lado dos reagentes​. Então, é preciso adicionar o coeficiente oito para o H₂O, no lado dos produtos, a fim de igualar a quantidade de átomos de hidrogênio em ambos os lados da equação. Assim, temos:

2 KMnO₄ + 16 HCl→ 2 KCl + 2 MnCl₂ ​+ 5 Cl₂ ​+ 8 H₂​O

• Passo 5: Agora, vamos verificar se todos os átomos estão balanceados:
  • K: Há dois átomos de potássio (K) em ambos os lados da equação.
  • Mn: Há dois átomos de manganês (Mn) em ambos os lados.
  • Cl: Há 16 átomos de cloro (Cl) no lado dos reagentes (16 HCl) e 16 átomos de cloro no lado dos produtos (2 KCl, 2 MnCl_2​, e 5 Cl₂​ — cada molécula de Cl₂​​ contém dois átomos de cloro, totalizando 10 átomos de Cl).
  • H: Há 16 átomos de hidrogênio (Hl) no lado dos reagentes (16 HCl) e 16 átomos de cloro no lado dos produtos (8 H₂O  — cada molécula de água contém dois átomos de hidrogênio, totalizando 16 átomos de H).
  • O: Há oito átomos de oxigênio no lado dos reagentes (2 KMnO_4​, que tem quatro oxigênios cada) e oito átomos de oxigênio no lado dos produtos (oito moléculas de água).

Após a verificação, o balanceamento estará concluído se for constatada a igualdade no número de átomos de cada elemento em ambos os lados da equação. Assim, a equação balanceada é:

2 KMnO₄ + 16 HCl→ 2 KCl + 2 MnCl₂ ​+ 5 Cl₂ ​+ 8 H₂​O

Regras para o balanceamento químico

O balanceamento de equações químicas é uma etapa essencial em qualquer reação, pois garante que as leis da conservação de massa e energia sejam respeitadas. Para realizar o balanceamento corretamente, é necessário seguir um conjunto de regras e uma ordem lógica ao considerar cada elemento presente na equação. Abaixo, estão as principais regras:

1. Conservar a quantidade de átomos de cada elemento: Em uma equação química balanceada, o número de átomos de cada elemento deve ser igual nos dois lados da equação (reagentes e produtos). Isso assegura que nenhum átomo seja perdido ou criado, conforme a lei da conservação das massas.
2. Escolher os coeficientes adequados: O balanceamento é feito ajustando os coeficientes, os números colocados à frente das fórmulas dos compostos, sem modificar as fórmulas químicas (isto é, sem alterar os subscritos). O objetivo é garantir que o número de átomos de cada elemento seja o mesmo em ambos os lados da equação.
3. Começar pelos elementos que aparecem em menor quantidade: É mais fácil balancear primeiro os elementos que aparecem em apenas um composto de cada lado da equação. Dessa forma, você pode ajustar os coeficientes sem afetar muito outras partes da equação.
4. Balancear primeiramente os metais e ametais: Os metais (quando presentes) devem ser balanceados primeiro, seguidos pelos ametais, deixando os átomos de hidrogênio e oxigênio por último. Isso porque hidrogênio e oxigênio costumam aparecer em mais de um composto, o que pode complicar o processo.
5. Usar frações e multiplicar para remover frações: Se, durante o balanceamento, for necessário utilizar números fracionários, faça isso para simplificar; mas, ao final, multiplique toda a equação por um número que elimine as frações.
6. Verificar o balanceamento total: Depois de balancear, sempre verifique se o número de átomos de cada elemento é o mesmo em ambos os lados da equação. Isso pode ser feito contando os átomos de cada elemento e comparando os reagentes com os produtos.

A ordem para considerar os elementos geralmente segue uma sequência para facilitar o processo balanceando, primeiro, os metais; depois, os ametais; e, por fim, hidrogênio e oxigênio. Lembrar-se dessa ordem ajudará a evitar confusões e retrabalhos.

Função do balanceamento químico

O balanceamento de equações químicas segue a lei de conservação das massas, enunciada por Antoine Lavoisier no século XVIII. Segundo essa lei, “em uma reação química, a massa total dos reagentes é igual à massa total dos produtos”. Isso significa que os átomos não desaparecem nem se transformam em novos elementos, apenas se reorganizam em diferentes compostos.

A importância dessa lei para a química está no fato de que ela permite prever, com precisão, a quantidade de substâncias que serão formadas em uma reação. Sem o balanceamento, não seria possível realizar cálculos estequiométricos, prever a eficiência das reações ou realizar experimentos controlados.

Macetes para fazer balanceamento químico

Um método muito utilizado para facilitar o balanceamento de equações químicas é a regra do Macho. Essa regra define a sequência em que os elementos devem ser balanceados e segue a seguinte ordem:

• M: Metais
• A: Ametais
• C: Carbono
• H: Hidrogênio
• O: Oxigênio

Essa sequência é particularmente útil porque facilita a memorização da sequência correta em que cada átomo deve ser balanceado. Além disso, deixa o oxigênio, que geralmente aparece em múltiplos compostos, para ser balanceado por último, facilitando o processo.

Vamos aplicar a regra do Macho na reação:

Na₂CO₃ + HCl → NaCl + H₂O + CO₂​

• Passo 1: Balancear os metais (Na)

No lado dos reagentes, temos dois átomos de sódio (Na₂CO₃​), enquanto, no lado dos produtos, temos apenas um átomo de sódio em NaCl. Portanto, multiplicamos o NaCl no lado dos produtos por 2:

Na₂CO₃ + HCl → 2 NaCl + H₂O + CO₂​

• Passo 2: Balancear os ametais (Cl)

No lado dos produtos, temos dois átomos de cloro em 2 NaCl, então, precisamos de dois átomos de cloro no lado dos reagentes. Para isso, multiplicamos o HCl por 2:

Na₂CO₃ + 2 HCl → 2 NaCl + H₂O + CO₂​

• Passo 3: Balancear o carbono (C)

Há um átomo de carbono em Na₂CO₃​ no lado dos reagentes e um átomo de carbono em CO₂​​ no lado dos produtos. Portanto, o carbono já está balanceado.

• Passo 4: Balancear o hidrogênio (H)

Há dois átomos de hidrogênio em 2 HCl no lado dos reagentes e dois átomos de hidrogênio em H₂O no lado dos produtos. O hidrogênio também está balanceado.

• Passo 5: Balancear o oxigênio (O)

Por fim, temos três átomos de oxigênio em Na₂CO₃​ no lado dos reagentes, enquanto, no lado dos produtos, temos dois átomos em CO₂ e um átomo em H₂O, totalizando três átomos de oxigênio. O oxigênio também está balanceado.

A equação balanceada final é:

Na₂CO₃ + 2 HCl → 2 NaCl + H₂O + CO₂​

A regra do Macho é um macete muito útil para lembrar a sequência dos elementos a serem balanceados, tornando o processo mais eficiente e garantindo que você siga uma lógica clara e precisa no balanceamento de equações químicas.

Saiba mais: Quais são os termos quantitativos mais importantes de uma equação química?

Exercícios resolvidos sobre balanceamento químico

Questão 1 (UFMG) A equação Ca(OH)₂ + H₃PO₄ → Ca₃(PO₄)₂ + H₂O não está balanceada. Balanceando-a com os menores números possíveis, a soma dos coeficientes estequiométricos será:

a) 4

b) 7

c) 10

d) 11

e) 12

Resposta: E. A soma dos coeficientes estequiométricos da equação balanceada é 12.

A regra do Macho é uma técnica útil para balancear equações químicas, pois facilita o método de tentativas e oferece uma maior agilidade na resolução.

Equação não balanceada: Ca(OH)₂ + H₃PO₄ → Ca₃(PO₄)₂ + H₂O

Passo a passo:

1. Metal: Começamos pelo cálcio (Ca). Nos produtos, temos três átomos de cálcio, enquanto, nos reagentes, temos apenas um. Para equilibrar, colocamos o coeficiente 3 antes do Ca(OH)₂:

3 Ca(OH)₂ + H₃PO₄ → Ca₃(PO₄)₂ + H₂O

2. Ametal: Agora, vamos equilibrar o fósforo (P). Nos produtos, temos dois átomos de fósforo, enquanto, nos reagentes, temos apenas um. Colocamos o coeficiente 2 antes do H₃PO₄:

3 Ca(OH)₂ + 2 H₃PO₄ → Ca₃(PO₄)₂ + H₂O

3. Carbono: Como não temos carbono nessa equação, pulamos essa etapa.
    
4. Hidrogênio: Agora, vamos equilibrar o hidrogênio (H). Nos reagentes, temos 12 átomos de hidrogênio (3 . Ca(OH)₂ + 2 . H₃PO₄), enquanto, nos produtos, temos apenas dois. Colocamos o coeficiente 6 antes da H₂O:

3 Ca(OH)₂ + 2 H₃PO₄ → Ca₃(PO₄)₂ + 6 H₂O

5. Oxigênio: Por fim, verificamos o oxigênio (O). Nos reagentes, temos 14 átomos de oxigênio (3 . Ca(OH)₂ + 2 . H₃PO₄), e, nos produtos, também temos 14 átomos de oxigênio (Ca₃(PO₄)₂ + 6 . H₂O).

Equação balanceada:

3 Ca(OH)₂ + 2 H₃PO₄ → 1 Ca₃(PO₄)₂ + 6 H₂O

Soma dos coeficientes estequiométricos: 3 + 2 + 1 + 6 = 12

Questão 2 (Enem) As mobilizações para promover um planeta melhor para as futuras gerações são cada vez frequentes. A maior parte dos meios de transporte de massa é atualmente movida pela queima de um combustível fóssil. A título de exemplificação do ônus causado por essa prática, basta saber que um carro produz, em média, cerca de 200 g de dióxido de carbono por km percorrido.

Revista Aquecimento Global. Ano 2, no 8. Publicação do Instituto Brasileiro de Cultura Ltda.

Um dos principais constituintes da gasolina é o octano (C₈H₁₈). Por meio da combustão do octano é possível a liberação de energia, permitindo que o carro entre em movimento. A equação que representa a reação química desse processo demonstra que:

a) no processo há liberação de oxigênio, sob a forma de O₂.

b) o coeficiente estequiométrico para a água é de 8 para 1 do octano.

c) no processo há consumo de água, para que haja liberação de energia.

d) o coeficiente estequiométrico para o oxigênio é de 12,5 para 1 do octano.

e) o coeficiente estequiométrico para o gás carbônico é de 9 para 1 do octano

Resposta: D

A equação balanceada da combustão do octano mostra que o coeficiente estequiométrico para o oxigênio é de 12,5 para 1 do octano.

1° passo: Montando a equação de combustão.

A combustão completa de um hidrocarboneto, como o octano, sempre resulta em dióxido de carbono (CO₂) e água (H₂O). A equação geral para essa reação é:

C₈H₁₈ + O₂ → CO₂ + H₂O

2° passo: Balanceando a equação.

Para balancear a equação, precisamos ajustar os coeficientes estequiométricos de forma que o número de átomos de cada elemento seja igual nos reagentes e nos produtos.

Começamos pelo carbono: como temos oito átomos de carbono no octano, precisamos de oito moléculas de CO₂:

C₈H₁₈ + O₂ → 8 CO₂ + H₂O

Agora, o hidrogênio: Temos 18 átomos de hidrogênio no octano, então precisamos de nove moléculas de H₂O:

C₈H₁₈ + O₂ → 8 CO₂ + 9 H₂O

Por fim, o oxigênio: Temos 16 átomos de oxigênio nos 8 CO₂ e nove átomos de oxigênio nas 9 H₂O, totalizando 25 átomos de oxigênio. Para balancear, precisamos de 25/2 moléculas de O₂:

C₈H₁₈ + 25/2 O₂ → 8 CO₂ + 9 H₂O

3° passo: Analisando as alternativas.

a) No processo há liberação de oxigênio, sob a forma de O₂: Falso. O oxigênio é um reagente, ou seja, é consumido na reação.

b) O coeficiente estequiométrico para a água é de 8 para 1 do octano: Falso. O coeficiente estequiométrico da água é 9, não 8.

c) No processo há consumo de água, para que haja liberação de energia: Falso. A água é um produto da reação, não um reagente.

d) O coeficiente estequiométrico para o oxigênio é de 12,5 para 1 do octano: Verdadeiro. Como 25/2 = 12,5, essa é a razão correta entre os coeficientes estequiométricos do oxigênio e do octano.

e) O coeficiente estequiométrico para o gás carbônico é de 9 para 1 do octano: Falso. O coeficiente estequiométrico do gás carbônico é 8, não 9.

Fontes

BROWN, Theodore L. et al. Química: a ciência central. 9 ed. São Paulo: Prentice Hall, 2005.

CHANG, Raymond. Química Geral: Conceitos Essenciais; 4ªed.; São Paulo: McGraw-Hill, 2007.