Cálculos estequiométricos no Enem

Os cálculos estequiométricos no Enem são cobrados de acordo com o tópico “Representação das transformações químicas” da Matriz de Referência do Enem. Os cálculos estequiométricos são formas de relacionar as quantidades de substâncias que reagem entre si e as quantidades das substâncias que são formadas em um processo reacional. Toda estequiometria de uma reação química pode ser percebida pela equação química devidamente balanceada. Os coeficientes estequiométricos das substâncias na equação química configuram a proporção molar mínima de reação entre os participantes.

Leia também: Como as forças intermoleculares são cobradas no Enem?

Tópicos deste artigo

• 1 - Resumo sobre os cálculos estequiométricos no Enem
• 2 - Como os cálculos estequiométricos são cobrados no Enem?
• 3 - O que são cálculos estequiométricos?
• 4 - Dicas para resolver os cálculos estequiométricos no Enem
• 5 - Questões sobre cálculos estequiométricos no Enem

Resumo sobre os cálculos estequiométricos no Enem

• Os cálculos estequiométricos no Enem são cobrados de acordo com o tópico “Representação das transformações químicas” da Matriz de Referência do Enem.

• Cálculos estequiométricos são formas de relacionar as quantidades das substâncias que reagem entre si e as quantidades das substâncias que são produzidas em processos químicos.

• A estequiometria de um processo deve ser avaliada por meio de uma equação química corretamente balanceada.

• Os coeficientes estequiométricos das substâncias nas equações químicas correspondem às mínimas proporções molares de reação.

Como os cálculos estequiométricos são cobrados no Enem?

Segundo a Matriz de Referência do Enem, disponibilizada pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep), em seus objetos de conhecimento, os cálculos estequiométricos são abordados da seguinte maneira:

Representação das transformações químicas - Fórmulas químicas. Balanceamento de equações químicas. Aspectos quantitativos das transformações químicas. Leis ponderais das reações químicas. Determinação de fórmulas químicas. Grandezas Químicas: massa, volume, mol, massa molar, constante de Avogadro. Cálculos estequiométricos. ^|1|

O que são cálculos estequiométricos?

Cálculos estequiométricos são formas de relacionar as quantidades das substâncias que reagem entre si e as quantidades de produtos que são formadas em processos reacionais. A estequiometria de uma reação química é avaliada a partir da análise da equação química, como a equação genérica a seguir:

a A + b B + ... → ... y Y + z Z

No caso, a partir da equação, percebe-se que, para cada “a” mols de A, são necessários “b” mols de B, entre outras substâncias possíveis, para formar “y” mols de Y e “z” mols de Z, entre outras. O problema, entretanto, é que nem sempre a relação entre as substâncias é conhecida, necessitando-se fazer ajustes na equação antes dos cálculos estequiométricos. Saiba mais detalhes sobre os cálculos estequiométricos clicando aqui.

Dicas para resolver os cálculos estequiométricos no Enem

Os exercícios de cálculos estequiométricos são distintos entre si, contudo, possuem em comum algumas etapas básicas de resolução que necessitam sempre de atenção:

1. Antes de se iniciar qualquer exercício, deve-se avaliar se a equação química está devidamente balanceada.

2. Nem todas as substâncias participantes entrarão no cálculo, assim, deve-se identificar quais deverão estar presentes no cálculo para evitar trabalho desnecessário.

3. Como os cálculos estequiométricos usam proporções, a ferramenta matemática mais usada é a regra de três simples. Contudo, deve-se atentar para o fato de que o mol e a massa de substâncias diferentes não apresentam proporção direta, e, por isso, não se deve operar a regra de três simples nessas condições, havendo necessidade de padronizar as unidades (todos os valores em mol ou todos os valores em massa, por exemplo).

4. Acima de tudo, a interpretação do problema é o mais difícil. Contudo, deve-se sempre avaliar questões importantes, como “Qual é o meu objetivo final nessa questão?”. Dessa forma, é possível alinhar a linha de raciocínio para tal.

5. Em uma estequiometria, sempre haverá uma substância participante que possui informações úteis (como uma massa ou um número de mols) e sempre haverá uma substância sobre a qual buscamos alguma informação. Geralmente, são essas duas que serão utilizadas no cálculo.

Veja também: Como fazer o balanceamento das equações químicas?

Questões sobre cálculos estequiométricos no Enem

Questão 1. (ENEM/2023) Um assistente de laboratório precisou descartar sete frascos contendo solução de nitrato de mercúrio (II) que não foram utilizados em uma aula prática. Cada frasco continha 5,25 g de Hg₂(NO₃)₂ dissolvidos em água. Temendo a toxicidade do mercúrio e sabendo que o Hg₂Cl₂ tem solubilidade muito baixa, o assistente optou por retirar o mercúrio da solução por precipitação com cloreto de sódio (NaCl), conforme a equação química:

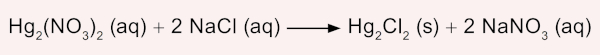
Na dúvida sobre a massa de NaCl a ser utilizada, o assistente aumentou gradativamente a quantidade adicionada em cada frasco, como apresentado no quadro.

O produto obtido em cada experimento foi filtrado, secado e teve sua massa aferida. o assistente organizou os resultados na forma de um gráfico que correlaciona a massa de NaCl adicionada com a massa de Hg₂Cl₂ obtida em cada frasco. A massa molar do Hg₂(NO₃)₂ é 525 g mol⁻¹, a do NaCl é 58 g mol⁻¹ e a do Hg₂Cl₂ é 472 g mol⁻¹.

Qual foi o gráfico obtido pelo assistente de laboratório?

A)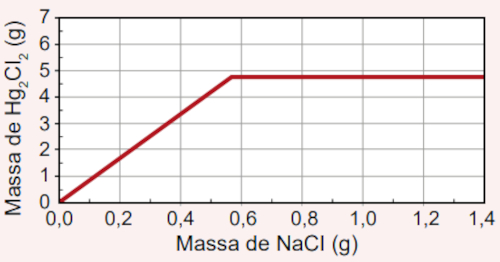

B)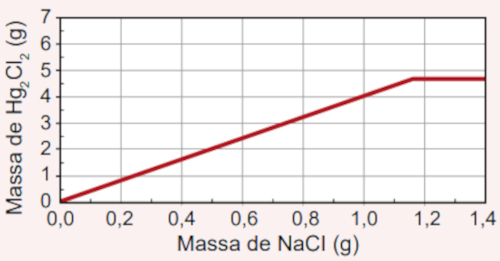

C)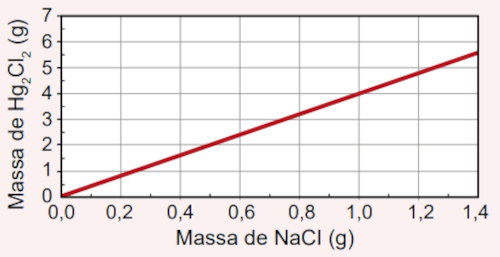

D)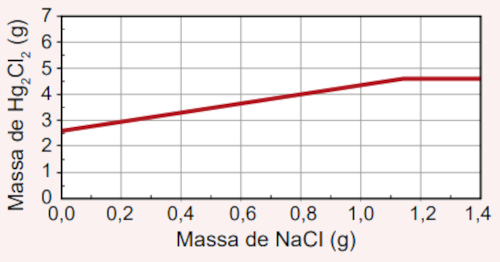

E)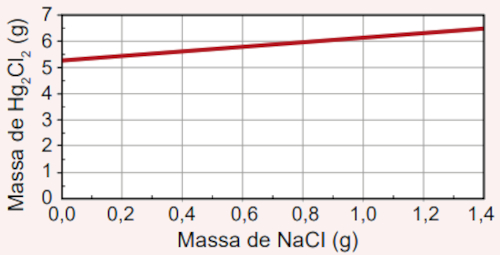

Resolução:

Alternativa B.

Como o assistente não sabe a massa de NaCl a ser utilizada, devemos entender que a reação será finalizada quando a massa de Hg₂Cl₂ produzida não sofrer mais alteração, mesmo que mais NaCl seja adicionado.

Segundo a reação química balanceada, para cada 1 mol de Hg₂(NO₃)₂, são necessários 2 mols de NaCl, produzindo, assim, 1 mol de Hg₂Cl₂.

O frasco continha 5,25 gramas de nitrato de mercúrio (II), o que, segundo a regra de três simples a seguir, corresponde a 0,01 mol dessa substância:

525 gramas Hg₂(NO₃)₂ --------------- 1 mol

5,25 gramas Hg₂(NO₃)₂ -------------- x

5,25 ⋅ 1 = 525 ⋅ x → x = 5,25/525 → x = 0,01 mol

Assim sendo, ao utilizar 0,01 mol de nitrato de mercúrio (II), utilizam-se 0,02 mol de NaCl e se produzem 0,01 mol de Hg₂Cl₂, proporcionalmente.

A massa molar do NaCl é de 58,5 g/mol e, assim, 0,02 mol corresponde a 1,17 gramas. Da mesma forma, a massa molar do Hg₂Cl₂ é igual a 472 g/mol e, por isso, 0,01 mol corresponde a 4,72 gramas.

Por isso, conclui-se que a máxima massa de Hg₂Cl₂ (4,72 gramas) é formada quando 1,17 gramas de NaCl são utilizados. Qualquer adição além de 1,17 gramas de NaCl não fará alteração sobre a massa de Hg₂Cl₂ produzido, visto que o Hg₂(NO₃)₂ será o reagente limitante e, por isso, já terá sido consumido, inviabilizando a continuidade da reação.

O gráfico que exprime essa condição é o da alternativa B, pois é possível perceber que a massa de Hg₂Cl₂ fica constante em 4,72 gramas após a massa de NaCl adicionado atingir os 1,17 gramas.

Questão 2

(Enem PPL 2023) Um carro sedã apresenta tipicamente 200 kg de alumínio distribuídos pelo chassi, motor e cabine. Uma amostra de bauxita, principal fonte natural do metal, é composta por 50% em massa de óxido de alumínio (Al₂O₃). Considere a massa molar do alumínio (Al) igual a 27 g mol⁻¹ e a do oxigênio (O) igual a 16 g mol⁻¹.

A massa de bauxita que deve ser empregada para produzir o alumínio usado na fabricação de um carro desse modelo é mais próxima de

A) 378 kg.

B) 400 kg.

C) 637 kg.

D) 756 kg.

E) 1 512 kg.

Resolução:

Alternativa D.

O alumínio oriundo da bauxita pode ser calculado por meio da simples decomposição do óxido de alumínio:

Al₂O₃ (s) → 2 Al (s) + ³/₂ O₂ (g)

O carro precisa de 200 kg de Al, assim, pode-se calcular a massa de Al₂O₃ necessária da seguinte forma:

1 mol Al₂O₃ ---------------- 2 mols Al

x ---------------------------- 200 kg de Al

Como não há proporcionalidade entre mol e massa de substâncias diferentes, deve-se padronizar as unidades por meio de uma regra de três simples, seja em mols, seja em unidades de massa. Como se deseja obter um valor de massa, entende-se que fica mais interessante converter os valores de mol para massa. Essa conversão só é possível com a massa molar, ou seja, a massa contida em 1 mol da substância.

A massa molar do Al₂O₃ é dada por:

2 ⋅ MM_Al + 3 ⋅ MM_O = 2 ⋅ (27) + 3 ⋅ (16) = 54 + 48 = 102 g mol⁻¹.

A regra de três simples convertida fica:

102 g de Al₂O₃ ------------- 2.27 g de Al

x ----------------------------- 200 kg

Não há problema em realizar a regra de três simples se a primeira linha está em gramas e a outra linha está em quilogramas, pois são unidades proporcionais. Contudo, como “x” está na linha dos quilogramas, ele terá essa unidade. Logo:

2 . 27 . x = 102 . 200

x ≈ 378 kg Al₂O₃

Como a bauxita corresponde à 50% de Al₂O₃, a massa de bauxita pode ser determinada se fazendo o seguinte raciocínio:

M_Bauxita ------------- 100 %

378 kg Al₂O₃ -------- 50%

M_Bauxita = 756 kg

Questão 3

(Enem PPL 2022) Os airbags de segurança dos automóveis são acionados com o impacto, que envia um sinal elétrico para o dispositivo e inicia a reação explosiva do trinitreto de sódio (NaN₃), produzindo sódio metálico e nitrogênio molecular, conforme a equação:

2 NaN₃ (s) → 2 Na (s) + 3 N₂ (g)

O gás produzido tem função de inflar o airbag. Esse tipo de dispositivo contém, aproximadamente, 100 g de NaN₃.

Considere: PV = nRT; P = 1 atm; T = 25 °C;

R = 0,0821 L∙atm/K∙mol; 0 °C = 273 K

Massas molares: NaN₃ = 65 g/mol; N₂ = 28 g/mol; Na = 23 g/mol

Nesse dispositivo, o volume de gás produzido, em litro, é

A) 4,7.

B) 9,4.

C) 18,8.

D) 56,5.

E) 113,0.

Resolução:

Alternativa D.

O gás produzido, conforme é perceptível na reação química, é o N₂ (é possível ver pelo “(g)”, que significa gás).

Pela estequiometria da reação, calcula-se a quantidade de N₂ produzida a partir dos 100 g de NaN₃ utilizados da seguinte forma:

2 mols NaN₃ ------------- 3 mols N₂

100 g NaN₃ -------------- x

Os valores de mol e de massa de substâncias diferentes não possuem relação de proporcionalidade, motivo pelo qual não se pode operar uma regra de três simples nessas condições. Por isso, deve-se padronizar as unidades, seja com todos os valores em mol, seja com todos os valores em unidade de massa. Como se deseja calcular um volume e, na equação dos gases ideais, há o parâmetro mol (representado pela letra “n”), entende-se que é mais confortável encontrar “x” em mol, assim, todos os valores devem ser convertidos para mol.

A conversão de massa para mol se dá pela massa molar (a massa contida em 1 mol da substância). Assim, calcula-se a massa molar de NaN3:

MM(NaN₃) = MM(Na) + 3∙MM(N) = 23 + 3∙14 = 23 + 42 = 65 g/mol

Assim, o número de mols em 100 gramas de NaN₃ é calculado:

\(n = \frac{m}{MM} \rightarrow n = \frac{100}{65} \rightarrow n \simeq 1,54 \, \text{mol} \)

A regra de três simples fica:

2 mols NaN₃ ---------------- 3 mols N₂

1,54 mols NaN₃ ------------- x

2 ∙ x = 1,54 ∙ 3 → x = 2,31 mols N₂.

Aplica-se, então, tal volume na expressão PV = nRT. A temperatura é dada em Kelvin, e, assim, como T = 25 °C, logo, T = 25 + 273 = 298 K. Substituindo-se os dados, temos:

\(PV = nRT \rightarrow 1 \cdot V = 2,31 \cdot 0,0821 \cdot 298 \rightarrow V \simeq 56,5 \, \text{L}\)

Questão 4

(Enem PPL 2021) Um marceneiro esqueceu um pacote de pregos ao relento, expostos à umidade do ar e à chuva. Com isso, os pregos de ferro, que tinham a massa de 5,6 g cada, acabaram cobertos por uma camada espessa de ferrugem (Fe₂O₃·H₂O), uma substância marrom insolúvel, produto da oxidação do ferro metálico, que ocorre segundo a equação química:

2 Fe (s) + ³/₂ O₂ (g) + H₂O (l) → Fe₂O₃·H₂O (s)

Considere as massas molares (g/mol): H = 1; O = 16; Fe = 56.

Qual foi a massa de ferrugem produzida ao se oxidar a metade (50%) de um prego?

A) 4,45 g.

B) 8,90 g.

C) 17,80 g.

D) 72,00 g.

E) 144,00 g.

Resolução:

Alternativa A.

A massa de ferro oxidada é a metade de 5,6 gramas, o que corresponde a 2,8 gramas. A questão solicita descobrir a massa de ferrugem produzida quando se utilizam 2,8 gramas de Fe. A estequiometria será feita da seguinte forma:

2 mols de Fe ------------- 1 mol Fe₂O₃·H₂O

2,8 g de Fe --------------- x

Porém, não há proporcionalidade entre mol e massa de substâncias diferentes, motivo pelo qual não se deve operar a regra de três simples nessas condições. Deve-se, então, padronizar a regra de três simples, colocando todas os valores em mols ou em unidades de massa. Como o objetivo final é encontrar uma massa, o caminho fica mais encurtado se os valores forem convertidos para massa. Para converter valores de mol para massa, utilizam-se as massas molares (a massa referente a 1 mol de substância).

A massa molar do Fe₂O₃·H₂O consiste no somatório da massa molar do Fe₂O₃ com H₂O, sendo calculado como:

(2 ⋅ MM_Fe + 3 ⋅ MM_O) + (2 ⋅ MM_H + MM_O) = (2 ⋅ 56 + 3 ⋅ 16) + (2 ⋅ 1 + 16) = 160 + 18 = 178 g/mol

Assim:

2 ⋅ 56 g de Fe --------------- 178 g de Fe₂O₃·H₂O

2,8 g de Fe ------------------ x

2 ⋅ 56 ⋅ x = 2,8 ⋅ 178

Como 28 é a metade de 56 (0,5 ⋅ 56 = 28), é possível perceber que 0,05 ⋅ 56 = 2,8. Dessa forma, o cálculo simplificado fica:

2 ⋅ x = 0,05 ⋅ 178 → x = 0,05 ⋅ 89 → x = 4,45 gramas

Questão 5

(Enem 2021) A obtenção de etanol utilizando a cana-de-açúcar envolve a fermentação dos monossacarídeos formadores da sacarose contida no melaço. Um desses formadores é a glicose (C₆H₁₂O₆), cuja fermentação produz cerca de 50 g de etanol a partir de 100 g de glicose, conforme a equação química descrita.

Em uma condição específica de fermentação, obtém-se 80% de conversão em etanol que, após sua purificação, apresenta densidade igual a 0,80 g/mL. O melaço utilizado apresentou 50 kg de monossacarídeos na forma de glicose.

O volume de etanol, em litro, obtido nesse processo é mais próximo de

A) 16.

B) 20.

C) 25.

D) 64.

E) 100.

Resolução:

Alternativa C.

A questão informa que 50 gramas de etanol são produzidos a partir de 100 gramas de glicose em uma proporção 1:2.

Assim sendo, ao utilizar 50 kg de glicose, como mostra no enunciado da questão, pode-se dizer que 25 kg de etanol são produzidos. Contudo, a conversão possui um rendimento de 80%, e, por isso, o etanol de fato produzido é igual a 80% de 25 kg, o que corresponde a 20 kg (0,8 ⋅ 25 = 20).

Entretanto, a questão solicita não a massa de etanol produzida nessas condições, mas sim o volume. Para tal, usamos a informação da densidade (0,8 g/mL).

0,8 g/mL equivale a 0,8 kg/L, proporcionalmente:

\(0,8 \, \frac{\text{g}}{\text{mL}} = 0,8 \, \frac{10^{-3} \, \text{kg}}{10^{-3} \, \text{L}} = 0,8 \, \frac{\text{kg}}{\text{L}} \)

Usando-se a fórmula da densidade, o volume de etanol encontrado é de 25 L:

\(d = \frac{m}{V} \rightarrow 0,8 \, \frac{\text{kg}}{\text{L}} = \frac{20 \, \text{kg}}{V} \rightarrow V = \frac{20}{0,8} \rightarrow V = 25 \, \text{L}\)

Notas

^|1| BRASIL. Matriz de Referência Enem. Ministério da Educação, Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Disponível em: https://download.inep.gov.br/download/enem/matriz_referencia.pdf.

Fontes

ATKINS, P.; JONES, L.; LAVERMAN, L. Princípios de Química: Questionando a vida e o meio ambiente. 7. ed. Porto Alegre: Bookman, 2018.

BRASIL. Matriz de Referência Enem. Ministério da Educação, Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Disponível em: https://download.inep.gov.br/download/enem/matriz_referencia.pdf.

IUPAC GOLD BOOK. Stoichiometry. Disponível em: https://goldbook.iupac.org/terms/view/S06026.