O que é a lei dos senos?

Quando é necessário relacionar um lado a um ângulo de um triângulo retângulo a fim de encontrar as medidas de um de seus lados ou de um de seus ângulos, podemos usar as relações trigonométricas: seno, cosseno e tangente. É possível calcular também a medida de um dos lados ou de um dos ângulos de um triângulo qualquer, isto é, não necessariamente de um triângulo retângulo. Para isso, um dos métodos utilizados é a lei dos senos.

Lei dos senos

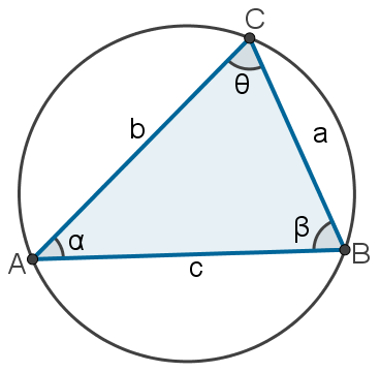
Considere como exemplo o triângulo ABC, inscrito em uma circunferência de raio r.

Em um caso como esse, os lados e ângulos possuem medidas quaisquer. Assim, temos:

   a   =      b   =     c     = 2r
senα     senβ     senθ       

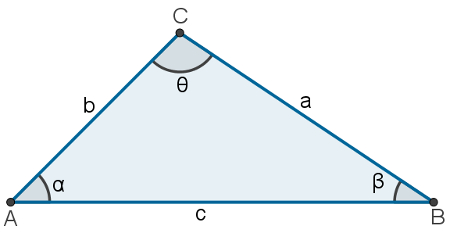
Nesse triângulo, a, b e c são as medidas de seus lados; α, β e θ são seus ângulos internos, e os senos desses ângulos têm os mesmos valores dos senos encontrados nas tabelas trigonométricas.

Na primeira fração, a é a medida do lado oposto ao senα; na segunda fração, b é a medida do lado oposto ao senβ, e, na terceira fração, note que c é a medida do lado oposto ao senθ. Portanto, existe uma proporção entre as razões formadas pela medida de um lado e o seno do ângulo oposto a essa medida.

Note também que cada uma dessas razões é igual ao diâmetro da circunferência que circunscreve o triângulo.

Na maioria das vezes em que for necessário calcular a medida de um lado de um triângulo, conhecendo as medidas de um ângulo oposto a ele, de outro lado e do ângulo oposto a esse outro lado, devemos usar a lei dos senos. Essa lei também pode ser usada para descobrir a medida de um dos ângulos de um triângulo, caso conheçamos as medidas de outro ângulo e dos lados opostos a esses dois ângulos.

Exemplos

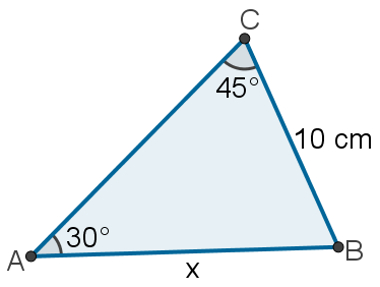
1 – Calcule a medida do lado AB no triângulo a seguir.

Observe que o lado AB, representado por x, é oposto ao ângulo de 45°, e o lado CB, que mede 10 cm, é oposto ao ângulo de 30°. Assim, podemos usar a lei dos senos:

    a      =      b    
  senα         senβ  

    x   =    10  
   sen45   sen30   

Usando a propriedade fundamental das proporções, temos:

x·sen30 = 10·sen45

Na tabela dos valores trigonométricos notáveis, sen45 = √2/2 e sen30 = 1/2. Substituindo esses valores, temos:

x = 10√2
2      2   

x = 10√2 cm

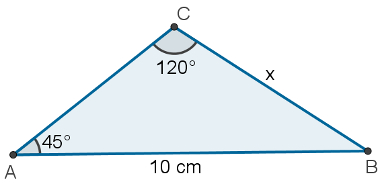
2 – Calcule a medida do lado CB no triângulo a seguir.

O lado CB, representado por x, é oposto ao ângulo de 45°. Observe também que o lado AB, que mede 10 cm, é oposto ao ângulo de 120°. Usando a lei dos senos, podemos escrever:

    a    =    b   
senα      senβ

    x     =   10    
sen45    sen120

x·sen120 = 10·sen45

Para continuar, lembre-se de que senx = sen(180 – x), portanto: sen120 = sen(180 – 120) = sen60. Substituindo o valor, temos:

x·sen60 = 10·sen45

x·√3 = 10·√2
  2           2

x·√3 = 10·√2

x = 10·√2
      √3

x = 10√3√2
      3

x = 10√6
      3

Por Luiz Paulo Moreira
Graduado em Matemática