Você sabe o que é semelhança de triângulos? A semelhança de triângulos ocorre quando dois triângulos têm seus ângulos correspondentes com mesma medida e seus lados proporcionais. Isso significa que um triângulo pode ser obtido do outro por meio de uma ampliação ou redução, sem que sua forma seja alterada.
Para determinar se dois triângulos são semelhantes, não é necessário comparar todos os lados e ângulos. Existem três casos de semelhança que permitem essa verificação de maneira mais eficiente. Caso AA (Ângulo-Ângulo): Se dois ângulos de um triângulo forem congruentes a dois ângulos de outro triângulo, então os triângulos são semelhantes. Caso LAL (Lado-Ângulo-Lado): Se dois lados de um triângulo são proporcionais a dois lados de outro triângulo e o ângulo formado por esses lados for congruente, então os triângulos são semelhantes. Caso LLL (Lado-Lado-Lado): Se os três lados de um triângulo são proporcionais aos três lados de outro triângulo, então os triângulos são semelhantes.
Esses casos são critérios que facilitam a identificação da semelhança entre triângulos sem a necessidade de medir todos os elementos. Além da semelhança entre triângulos, existe a congruência. Dois triângulos são congruentes quando eles têm ângulos e lados correspondentes com as mesmas medidas.
Leia também: Qual é a classificação dos triângulos?
Tópicos deste artigo
- 1 - Resumo sobre semelhança de triângulos
- 2 - Casos de semelhança de triângulos
- 3 - Como se calcula semelhança de triângulos?
- 4 - Teorema fundamental da semelhança de triângulos
- 5 - Congruência de triângulos x semelhança de triângulos
- 6 - Relações métricas no triângulo retângulo
- 7 - Exercícios resolvidos sobre semelhança de triângulos
Resumo sobre semelhança de triângulos
- Semelhança de triângulos é a situação em que dois triângulos têm seus ângulos correspondentes com mesma medida e seus lados proporcionais.
- Um triângulo pode ser obtido do outro por ampliação ou redução sem alterar sua forma, gerando triângulos semelhantes.
- Existem critérios de semelhança que nos auxiliam a identificar triângulos semelhantes.
- Os casos de semelhança são:
- AA (Ângulo-Ângulo): Dois ângulos correspondentes iguais garantem a semelhança.
- LAL (Lado-Ângulo-Lado): Dois lados proporcionais e o ângulo entre eles congruente garantem a semelhança.
- LLL (Lado-Lado-Lado): Três lados proporcionais garantem a semelhança.
- Esses critérios permitem verificar a semelhança sem medir todos os elementos dos triângulos.
- Dois triângulos são congruentes quando têm ângulos e lados correspondentes com as mesmas medidas.
Casos de semelhança de triângulos
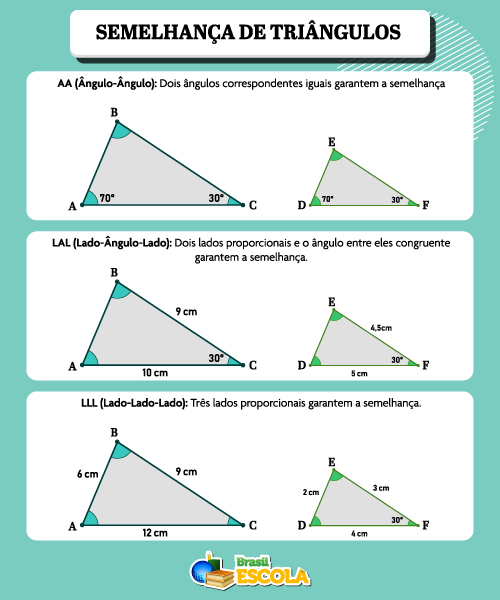
Existem três casos de semelhança de triângulos, veremos, a seguir, cada um deles.
→ Caso Ângulo-Ângulo (AA)
Dois triângulos são semelhantes se dois ângulos de um triângulo forem congruentes a dois ângulos do outro triângulo. Se dois ângulos correspondentes são congruentes, os triângulos são semelhantes. Da mesma forma, se dois triângulos são semelhantes, então seus ângulos correspondentes são congruentes.
- Exemplo:
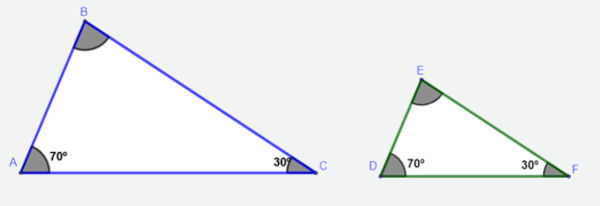
Os triângulos ABC e DEF são semelhantes por terem dois ângulos internos congruentes entre si.
→ Caso Lado-Ângulo-Lado (LAL)
Dois triângulos são semelhantes se dois lados correspondentes forem proporcionais e o ângulo formado entre eles for congruente. Se os lados correspondentes têm a mesma razão de proporcionalidade e o ângulo entre eles é igual, então os triângulos são semelhantes.
- Exemplo:
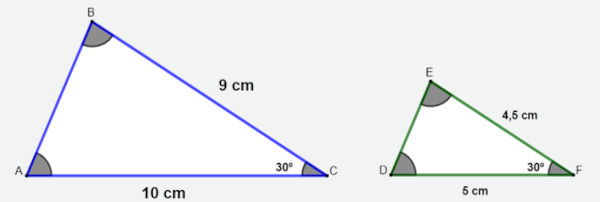
Os triângulos ABC e DEF são semelhantes, pois note que a medida dos lados conhecidos do triângulo ABC mede o dobro da medida do lado do triângulo DEF, assim, temos que:
\(\frac{\overline{AC}}{\overline{DF}} = \frac{10}{5} = 2 \\ \frac{\overline{BC}}{\overline{EF}} = \frac{9}{4.5} = 2 \)
Note também que os ângulos entre esses lados nos dois triângulos são de 30º, ou seja, têm a mesma medida, sendo assim, esses triângulos são semelhantes pelo caso LAL.
→ Caso Lado-Lado-Lado (LLL)
Dois triângulos são semelhantes se os três lados de um triângulo forem proporcionais aos três lados do outro triângulo. Se cada lado de um triângulo tem a mesma razão de proporcionalidade com os lados correspondentes de outro triângulo, então os triângulos são semelhantes.
- Exemplo:
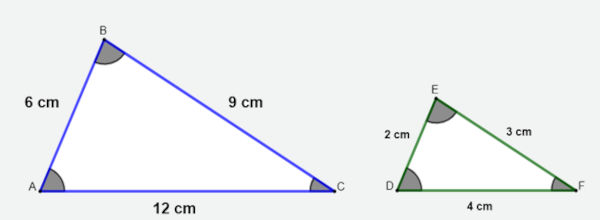
Podemos observar que os lados correspondentes têm a mesma proporção:
\(\frac{12}{4} = \frac{9}{3} = \frac{6}{2} = 3 \)
Logo, os triângulos ABC e DEF são semelhantes.
Fórmula da semelhança no triângulo
Como os dois triângulos têm lado proporcional, dados os triângulos ABC semelhantes ao triângulo DEF, então temos que:
\(\frac{\overline{AB}}{\overline{DE}} = \frac{\overline{BC}}{\overline{EF}} = \frac{\overline{AC}}{\overline{DF}} = k \\ \)
Em que k é um número real conhecido também como constante de proporcionalidade. Por exemplo, dados dois triângulos, sabemos que a medida dos lados do primeiro é o dobro da medida dos lados do segundo, então a constante de proporcionalidade será igual a dois.
Como se calcula semelhança de triângulos?
A semelhança de triângulo é utilizada para encontrar medidas desconhecidas no triângulo, já que triângulos semelhantes têm lados que são proporcionais. Veremos, a seguir, algumas aplicações.
- Exemplo 1:
Encontre a medida do lado DF, representada por x, do triângulo a seguir:
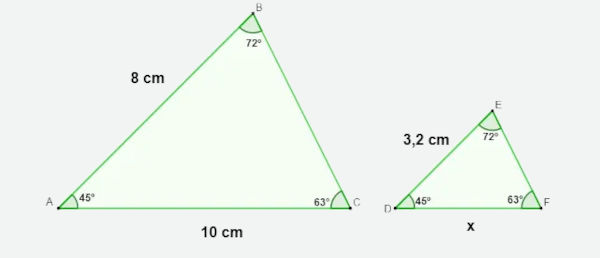
Resolução:
Analisando os triângulos, é possível perceber que os ângulos são congruentes, logo, temos um caso de semelhança Ângulo-Ângulo. Sabemos que a razão entre os lados correspondentes nesses triângulos é a mesma, logo, temos que:
\(\frac{8}{3.2} = \frac{10}{x} \\ \)
Multiplicando cruzado:
\(8x = 10 \cdot 3,2 \\ 8x = 32 \\ x = \frac{32}{8} \\ x = 4\ \text{cm} \)
- Exemplo 2:
Encontre o valor de x no triângulo a seguir:
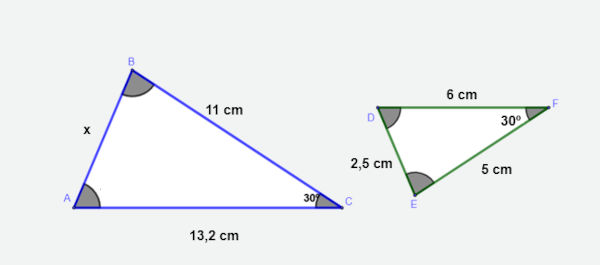
Resolução:
Analisando os triângulos, podemos perceber que há um ângulo congruente, agora verificaremos se os lados que formam esses ângulos são proporcionais. Como o maior lado do triângulo ABC é AC, e o maior lado do triângulo DEF é DF, então eles serão correspondentes:
\(\frac{AC}{DF} = \frac{BC}{EF} \\ \frac{13,2}{6} = \frac{11}{5} = 2,2 \)
Assim, esses triângulos são proporcionais pelo caso LAL e o coeficiente de proporcionalidade é 2,2, logo, temos que:
\(\frac{x}{2,5} = 2,2 \\ x = 2,2 \cdot 2,5 \\ x = 5,5\ \text{cm} \)
Teorema fundamental da semelhança de triângulos
O teorema fundamental da semelhança de triângulos afirma que: se uma reta transversal a dois lados de um triângulo for paralela ao terceiro lado, então ela determina um segundo triângulo, semelhante ao triângulo original. É possível perceber que a semelhança ocorre porque os ângulos correspondentes dos dois triângulos são congruentes, garantindo o critério AA (Ângulo-Ângulo) de semelhança. Além disso, os lados correspondentes desses triângulos são proporcionais.
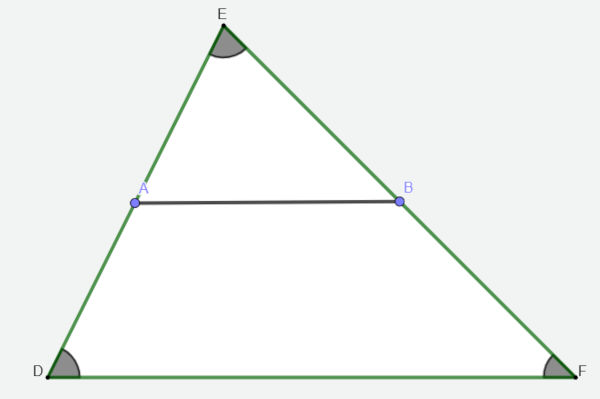
Traçando o segmento de reta AB, sendo ele paralelo ao segmento de reta DF, note na imagem que temos dois triângulos, o triângulo ABE e o triângulo DFE. Esses triângulos são congruentes, pois os ângulos da base do triângulo DFE são congruentes aos ângulos da base do triângulo ABE.
Congruência de triângulos x semelhança de triângulos
Além da semelhança de triângulos, existe a congruência de triângulos. O que as diferencia é que dois triângulos serão semelhantes se tiverem lados proporcionais e ângulos congruentes; enquanto dois triângulos serão congruentes se eles tiverem lados e ângulos congruentes. Enquanto os casos de semelhança de triângulos são AA (Ângulo-Ângulo) LAL (Lado-Ângulo-Lado) e LLL (Lado-Lado-Lado), os casos de congruência de triângulos são LLL (Lado-Lado-Lado), LAL (Lado-Ângulo-Lado), ALA (Ângulo-Lado-Ângulo) e LAA (Lado-Ângulo-Ângulo).
Relações métricas no triângulo retângulo
As relações métricas no triângulo retângulo são equações que relacionam os lados e as projeções dos catetos na hipotenusa. Elas são fundamentais para a resolução de problemas envolvendo triângulos retângulos, principalmente na geometria e na trigonometria.
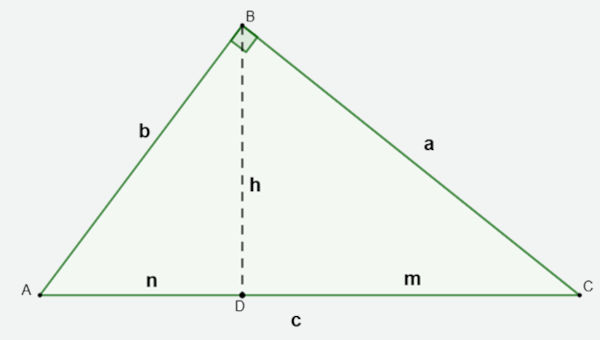
- c → medida da hipotenusa (lado oposto ao ângulo de 90º)
- a → cateto
- b → cateto
- h → altura relativa à hipotenusa
- m → projeção do cateto a sobre a hipotenusa
- n → projeção do cateto b sobre a hipotenusa
Dado o triângulo retângulo, as relações métricas são:
- a2 + b2 = c2
- h2 = m · n
- b2 = c · n
- a2 = c · m
- c · h = a · b
Essas relações são utilizadas para calcular medidas em triângulos retângulos sem precisar aplicar diretamente a trigonometria.
Exercícios resolvidos sobre semelhança de triângulos
Questão 1
Analisando o triângulo a seguir, sabendo que DE é paralelo a CB, então o valor de x é:
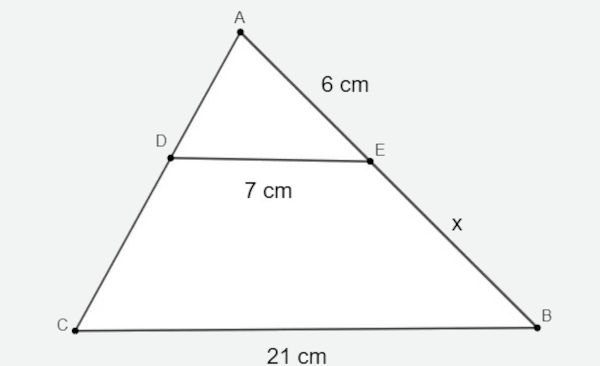
A) 10 cm
B) 12 cm
C) 14 cm
D) 16 cm
E) 18 cm
Resolução:
Alternativa B.
Pelo teorema fundamental da semelhança, sabemos que os triângulos ABC e ADE são semelhantes.
Logo, temos que:
\(\frac{21}{7} = \frac{x + 6}{6} \\ \)
Multiplicando cruzado:
\(7(x + 6) = 21 \cdot 6 \\ 7x + 42 = 126 \\ 7x = 126 - 42 \\ 7x = 84 \\ x = \frac{84}{7} \\ x = 12\ \text{cm} \)
Questão 2
Em uma cidade, um engenheiro deseja calcular a altura de uma torre de transmissão utilizando um método de comparação de sombras. No mesmo momento do dia, um poste de iluminação de 4 metros projeta uma sombra de 2,5 metros, enquanto a sombra da torre mede 20 metros.
Com base nessas informações, determine a altura da torre.
A) 28 m
B) 30 m
C) 32 m
D) 34 m
E) 36 m
Resolução:
Alternativa C.
Podemos representar a situação por meio de uma imagem:
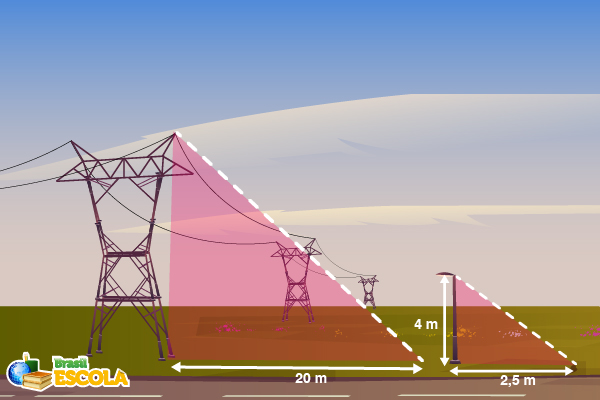
Como o Sol incide formando o mesmo ângulo tanto no poste quanto na torre de transmissão, esses triângulos são semelhantes pelo caso Ângulo-Ângulo. Como eles têm lados proporcionais, temos que:
\(\frac{x}{4} = \frac{20}{2,5} \\ 2,5x = 20 \cdot 4 \\ 2,5x = 80 \\ x = \frac{80}{2,5} \\ x = 32 \)
Fonte
DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. 1. ed. São Paulo: Ática, 2005. 3 v.

