O que é logaritmo?

Definição de logaritmo

Dados os números reais a e b, positivos e com a diferente de 1, existe um único número real x que fará a seguinte afirmação ser verdadeira:

a^x = b

O número x, nesse caso, é conhecido como logaritmo de b na base a. A palavra logaritmo pode ser substituída pela palavra expoente, assim, poderíamos escrever que x é o expoente de b na base a.

Veja a representação dessa definição:

Log_a b = x

Logo, podemos escrever a seguinte equivalência:

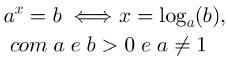
No caso acima, as letras utilizadas representam números e estamos interessados em descobrir o valor numérico da letra x. Essas letras recebem as seguintes denominações:

a é chamado de base do logaritmo;

b é chamado de logaritmando;

x é chamado de logaritmo.

Propriedades dos logaritmos

As propriedades de 1 a 5, dispostas a seguir, são corolários (consequências diretas) da definição de logaritmos dada acima. As propriedades de 6 a 8 são as propriedades operatórias dos logaritmos. Confira:

• O logaritmo de 1, em qualquer base, é sempre igual a zero, pois todo número elevado a zero é igual a 1.

  Não pare agora... Tem mais depois da publicidade ;)

Log_a 1 = 0

• O logaritmo em que o logaritmando e a base são iguais resulta em 1, pois todo número elevado a 1 é igual a ele mesmo.

Log_a a = 1

• O logaritmo cujo logaritmando é igual à base, mas está elevado a um número qualquer, tem esse número como resultado.

Log_a a^m = m

• Se os logaritmos de dois números na mesma base são iguais, então, esses dois números também são.

Log_a c = Log_a d, então, c = d

• Quando o logaritmo de b na base a for expoente do próprio a, o resultado será o próprio b.

a^{loga b} = b

• O logaritmo do produto é igual à soma dos logaritmos.

Log_a (k·h) = Log_a k + Log_a h

• O logaritmo da razão é igual à diferença dos logaritmos.

Log_a x = Log_a x – Log_a y
y                   

• No logaritmo de uma potência, o expoente “cai” e é multiplicado pelo logaritmo.

Log_a k^m = m·Log_a k

Por Luiz Paulo Moreira
Graduado em Matemática