Baricentro de um triângulo

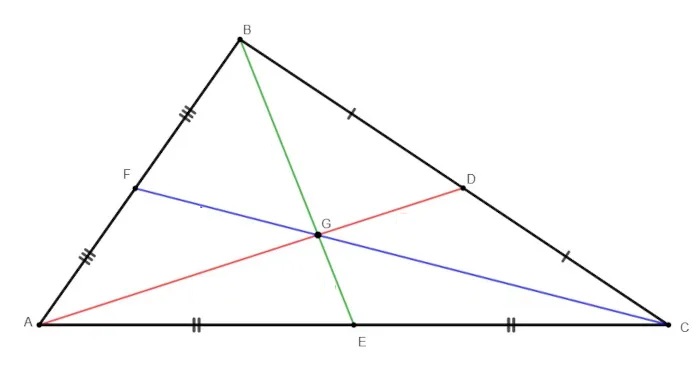
O baricentro é um dos pontos notáveis do triângulo, que, por sua vez, é um dos mais simples polígonos conhecidos. Essa figura geométrica é vastamente estudada, e um dos pontos que merecem atenção é o conceito de baricentro.

Conhecemos como baricentro o centro de gravidade do triângulo. Para encontrá-lo, é necessário determinar as suas três medianas, bem como o ponto de encontro entre elas. Quando o triângulo está representado no plano cartesiano, para encontrar o baricentro, basta calcular a média aritmética entre os valores de x e de y para encontrar o par ordenado do baricentro.

Leia também: Como os triângulos são classificados?

Tópicos deste artigo

• 1 - O que é o baricentro?
• 2 - Propriedades do baricentro
• 3 - Como se calcula o baricentro?
• 4 - Exercícios resolvidos

O que é o baricentro?

O triângulo possui pontos importantes, conhecidos como pontos notáveis, e o baricentro é um deles, junto com o circuncentro, o incentro e o ortocentro. O baricentro é o centro de gravidade do triângulo e é representado pela letra G. Ele está localizado no encontro das medianas do triângulo.

A mediana de um triângulo é um segmento que parte de um vértice e vai até o ponto médio do lado oposto a esse vértice. Em um triângulo qualquer, é possível traçar as três medianas, cada uma delas partindo de um dos vértices.

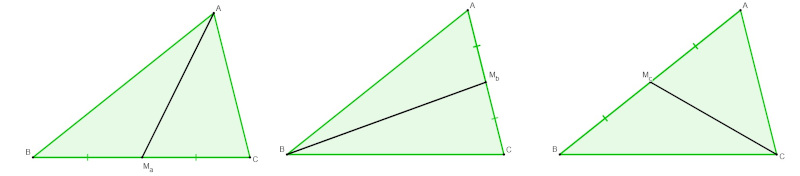
Quando traçamos simultaneamente as três medianas, as três se encontram em um único ponto. Esse ponto, representado por G, é o baricentro.

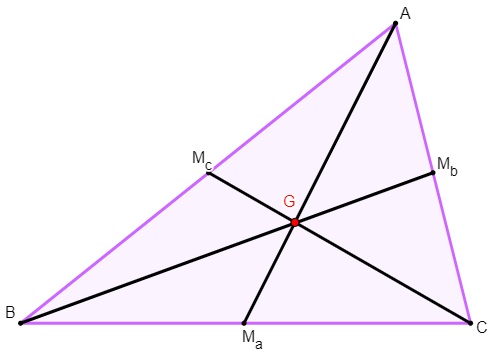
Propriedades do baricentro

• Propriedade 1: o baricentro é sempre um ponto interno do triângulo.

Como a mediana é sempre um segmento interno do triângulo, consequentemente o baricentro também é, independentemente da sua forma.

• Propriedade 2: o baricentro divide a mediana em duas partes cuja razão é 1:2.

Analisando o triângulo representado anteriormente, temos que:

Como se calcula o baricentro?

Quando representado no plano cartesiano, é possível encontrar as coordenadas do baricentro do triângulo. Para isso, vamos calcular a média aritmética dos valores de x e também dos valores de y.

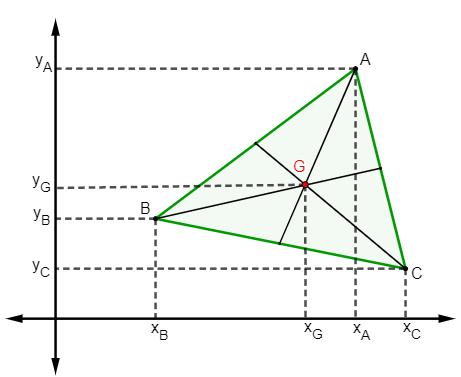
Note que os vértices são A (x_A, y_A), B(x_B, y_B) e C (x_C, y_C), então, para encontrar as coordenadas do baricentro G (x_G, y_G), utilizamos a fórmula:

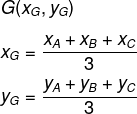
Veja também: Trigonometria em um triângulo qualquer

Exercícios resolvidos

Questão 1 – Podemos afirmar que o baricentro do triângulo cujos vértices são os pontos A(2,1), B (- 3, 5) e C (4,3) é o ponto:     

A) G (1,3).

B) G (3,1).

C) G (3,3).

D) G (-2,-1).

E) G ( -1,3).

Resolução

Alternativa A. Para encontrar as coordenadas do baricentro do triângulo, vamos calcular a média aritmética entre os valores de x nos pontos A, B e C e entre os valores de y nos mesmos pontos.

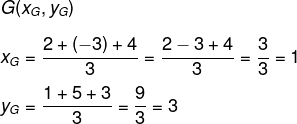
Sendo assim, o baricentro é o ponto G (1,3).

Questão 2 – Em uma cidade, serão instaladas três torres de telefonia para resolver o problema com a falha na rede e no sinal para os celulares. Acontece que as posições dessas torres foram planejadas de modo que o centro da cidade coincida com o baricentro do triângulo com vértices em A, B e C, que são as localizações das torres. Para escolher a posição das torres, definiu-se a prefeitura como a origem do eixo, e o centro da cidade se localiza no ponto (1,-1). Certificaram-se que as localizações dos pontos A e B seriam A(12, -6), B(-4,-10). Sendo assim, qual deve ser a localização do ponto C?

A) (3,8)
B) (8,-13)
C) (3,8)
D) (-5, 13)
E) (-5, 8)

Resolução

Alternativa D. Sabemos que G é a localização do centro da cidade, que é o ponto de coordenadas (1,-1).

Seja (x,y) as coordenadas do ponto C, então:

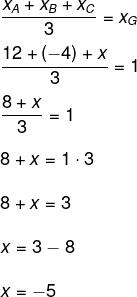
Encontrando também o valor de y:

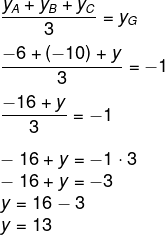
Desse modo, chegamos a C (-5, 13).

Por Raul Rodrigues de Oliveira
Professor de Matemática