Racionalização de denominadores é a técnica utilizada quando uma fração tem um número irracional no denominador e se deseja encontrar uma segunda fração equivalente à primeira fração, mas que não tenha um número irracional em seu denominador. Para fazer isso, é necessário realizar operações matemáticas para reescrever a fração de forma que ela não tenha em seu denominador uma raiz não exata.
Leia também: Como resolver operações com frações?
Tópicos deste artigo
Como fazer a racionalização de denominadores?
Começaremos pelo caso mais simples de racionalização de denominadores e seguiremos até o mais complexo, mas a técnica em si consiste em buscar uma fração equivalente multiplicando o numerador e o denominador por um número conveniente que permita eliminar a raiz do denominador da fração. Veja como fazer isso em diferentes situações a seguir.
-
Racionalização quando há uma raiz quadrada no denominador
Existem algumas frações que podem ser representadas com números irracionais nos denominadores. Veja alguns exemplos:
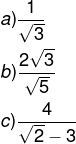
Quando o denominador da fração é irracional, utilizamos algumas técnicas para transformá-lo em um denominador racional, como a racionalização. Quando há uma raiz quadrada no denominador, podemos dividir em dois casos. O primeiro deles é quando a fração possui apenas uma raiz em seu radical.
Exemplo 1:
![]()
Para racionalizar esse denominador, vamos encontrar a fração equivalente a essa, mas que não tenha um denominador irracional. Para isso, vamos multiplicar o numerador e o denominador por um mesmo número — nesse caso, será exatamente o denominador da fração, ou seja, √3.
![]()
Na multiplicação de frações, multiplicamos reto. Sabemos que 1 · √3 = √3. Já no denominador, temos que √3 ·√3 = √9 = 3. Com isso, chegamos ao seguinte:
![]()
Logo, temos uma representação da fração cujo denominador não é um número irracional.
Exemplo 2:
O segundo caso é quando existe uma adição ou uma diferença entre uma raiz não exata.
![]()
Quando há no denominador uma diferença ou uma adição de termos, sendo um deles a raiz não exata, multiplicamos o numerador e o denominador pelo conjugado do denominador. Chamamos de conjugado de √2 – 1 o inverso do segundo número, isto é, √2 + 1.
![]()
Realizando a multiplicação no numerador, temos que:
3(√2 + 1) = 3√2 +3
Já o denominador é o produto notável conhecido como produto da soma pela diferença. O seu resultado sempre é o quadrado do primeiro termo menos o quadrado do segundo termo.
(√2 – 1)(√2 + 1) = √2² – 1²
(√2 – 1)(√2 + 1) = √4 – 1²
(√2 – 1)(√2 + 1) = 2 – 1
(√2 – 1)(√2 + 1) = 1
Então, racionalizando o denominador dessa fração, temos que:
![]()
Veja também: Três erros comuns na simplificação de fração algébrica
-
Racionalização quando há uma raiz de índice maior que 2
Agora veja alguns exemplos quando há no denominador uma raiz de índices maiores que 2.
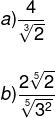
Como o objetivo é eliminar o radical, vamos multiplicar o denominador, de forma que a raiz desse denominador possa ser cancelada.
Exemplo 1:
![]()
Nesse caso, para eliminar o expoente do radical, vamos multiplicar pela raiz cúbica de 2² no numerador e no denominador, para que apareça dentro do radical 2³ e, assim, seja possível cancelar a raiz cúbica.
![]()
Realizando a multiplicação, temos que:
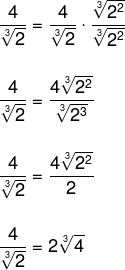
Exemplo 2:
![]()
Utilizando o mesmo raciocínio, vamos multiplicar o denominador e o numerador por um número que faça com que a potência do denominador chegue até o índice, ou seja, vamos multiplicar por raiz quinta de 3 ao cubo para que seja possível cancelar o denominador.
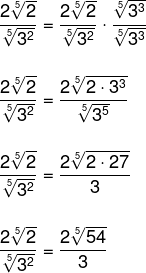
Leia também: Como simplificar frações algébricas?
Exercícios resolvidos
Questão 1 – Racionalizando o denominador da fração a seguir, encontramos:
![]()
A) 1 + √3.
B) 2(1 + √3).
C) – 2(1+ √3).
D) √3.
E) √3 –1.
Resolução
Alternativa C.
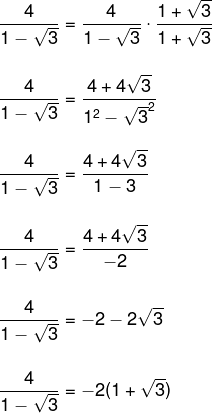
Questão 2 – (IFCE 2017 — adaptada) Aproximando os valores de √5 e √3 até a segunda casa decimal, obtemos 2,23 e 1,73, respectivamente. Aproximadamente, o valor da expressão numérica a seguir até a segunda casa decimal é:
![]()
A) 1,98.
B) 0,96.
C) 3,96.
D) 0,48.
E) 0,25.
Resolução
Alternativa E.
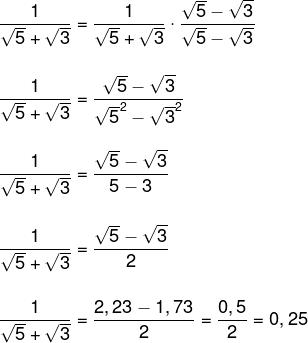
Por Raul Rodrigues de Oliveira
Professor de Matemática



