A multiplicação de frações pode ser, à primeira vista, algo desafiador, por se tratar de uma multiplicação de números que estão sendo divididos, porém seu cálculo é simples e bastante rápido, ao contrário do que se imagina, pois sua resolução não leva em conta o quociente da fração.
Leia também: Simplificação de fração: saiba como fazer
Tópicos deste artigo
- 1 - Como se faz multiplicação com frações?
- 2 - Jogo de sinais na multiplicação de frações
- 3 - Exercício resolvido
Como se faz multiplicação com frações?
As frações fazem parte do conjunto de números racionais. Esse conjunto pode ser escrito da seguinte maneira:
![]()
O conjunto dos números racionais possuem operações muito bem definidas, ou seja, ao utilizar dois números desse conjunto em qualquer uma das operações fundamentais, inclusive a multiplicação, o resultado também será um número racional.
A multiplicação de frações é realizada multiplicando o numerador da primeira fração com o numerador da segunda fração e em seguida multiplicando o denominador da primeira com o denominador da segunda. A operação continua sucessivamente em casos em que a multiplicação envolvem mais de duas frações.
Veja a forma geral.
Seja a, b, c e d números inteiros com b ≠ 0 e d ≠ 0, então é válido que:
![]()
→ Exemplos
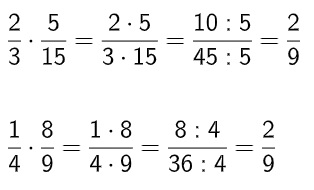
Jogo de sinais na multiplicação de frações
O numerador e o denominador são números inteiros, logo, as frações herdam algumas propriedades desse conjunto, como o jogo de sinais:
|
Sinal do primeiro número |
Sinal do segundo número |
Sinal do resultado |
|
+ |
+ |
+ |
|
+ |
- |
- |
|
- |
+ |
- |
|
- |
- |
+ |
Saiba também: Fração equivalente: o que é?
Exercício resolvido
Questão 1 – Sabe-se que o produto entre as razões entre x e 4, e, 5 e 2 é igual a 30. Determine o valor de x.
Solução
Devemos efetuar a multiplicação entre as razões, logo:
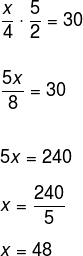
Por Robson Luiz
Professor de Matemática

