Comprimento da circunferência

O comprimento de uma circunferência é a medida do seu contorno. Essa medida é chamada de perímetro em outras figuras geométricas, como o triângulo, quadrado e retângulo, e depende dos lados da figura. No caso da circunferência, seu comprimento depende apenas do raio.

Veja também: Quais são as medidas de comprimento?

Tópicos deste artigo

• 1 - Resumo sobre comprimento de uma circunferência
• 2 - O que é comprimento da circunferência?
• 3 - Como se calcula o comprimento da circunferência?
• 4 - Exercícios resolvidos sobre comprimento da circunferência

Equação geral da circunferência

Saiba mais

Posições relativas entre um ponto e uma circunferência

Saiba mais

Resumo sobre comprimento de uma circunferência

• A medida do contorno de uma circunferência é conhecida como o comprimento da circunferência.

• A relação entre uma circunferência e seu comprimento pode ser associada à relação entre um polígono e seu perímetro.

• A fórmula para calcular o comprimento C de uma circunferência de raio r é

$C = 2πr$

O que é comprimento da circunferência?

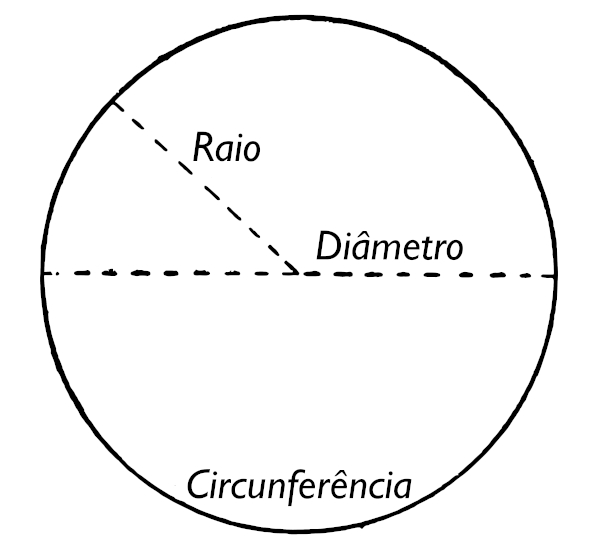
O comprimento de uma circunferência é a medida do contorno dessa figura. Lembre-se de que uma circunferência é formada por um conjunto de pontos que possuem a mesma distância de determinado ponto, chamado de centro. Essa distância é chamada de raio, e o dobro do raio é chamado de diâmetro.

Importante: Alguns textos se referem ao comprimento da circunferência como perímetro do círculo, pois o contorno (ou borda) de um círculo de raio r é uma circunferência de raio r.

Como se calcula o comprimento da circunferência?

Para calcular o comprimento C de uma circunferência de raio r, utilizamos a seguinte fórmula:

$C = 2πr$

Alguns textos apresentam essa expressão na forma $C = dπ$, em que d é o diâmetro da circunferência. Perceba que podemos escrever $C = 2πr$ como $C = 2rπ$, ou seja, $C = dπ$.

Importante: O comprimento de uma circunferência deve ser expresso na mesma unidade de medida que o raio dessa circunferência.

A seguir, veremos dois exemplos de como calcular o comprimento da circunferência.

• Exemplo 1:

Qual o comprimento de uma circunferência com 4 cm de raio? (Considere π = 3)

Resolução:

Aplicando a fórmula para r = 4 cm e realizando a aproximação indicada para o valor de π, temos que

$C = 2πr = 2⋅3 ⋅4 =24\ cm$

• Exemplo 2:

Um barbante possui 30 cm de comprimento. Ao unir as duas pontas, é possível formar uma circunferência com qual diâmetro? (Considere π =  3)

Resolução:

Aplicando a fórmula para C = 30 cm e realizando a aproximação indicada para o valor de π, temos que

$C = 2πr$

$30 = 2⋅3 ⋅r$

$r=\frac{30}6=5\ cm$

Assim, o diâmetro da circunferência mede 10 cm.

Veja também: Qual é a área do círculo?

Exercícios resolvidos sobre comprimento da circunferência

Questão 1

(Fundatec) Saulo comprou uma frigideira circular com diâmetro medindo 30 cm. Para fazer uma receita, ele precisou saber o comprimento da circunferência dessa frigideira. Ao realizar o cálculo, chegou à conclusão de que o comprimento correto da circunferência dessa frigideira é de: (Utilize π = 3,14)

A) 47,10 cm

B) 90 cm

C) 94,2 cm

D) 188,40 cm

E) 706,5 cm

Resolução:

Alternativa C.

Como o diâmetro da frigideira mede 30 cm, segue que o raio mede 15 cm. Assim, utilizando a expressão para o comprimento de uma circunferência, temos que

$C = 2πr$

$C = 2⋅3,14 ⋅15$

$C = 94,2\ cm$

Questão 2

(Fundatec) A terça parte do raio de uma circunferência com comprimento igual a 18,84 cm, considerando π = 3,14, é igual a:

A) 1 cm

B) $\frac{1}2$ cm

C) $\frac{1}3$ cm

D) 2 cm

E) 3 cm

Resolução:

Alternativa A.

Aplicando C = 18,84 cm e π = 3,14 na expressão do comprimento de uma circunferência, temos que

$C = 2πr$

$18,84 = 2⋅3,14 ⋅r$

$r=\frac{18,84}{6,28}=3$

Portanto, a terça parte de r é igual a $\frac{1}3 ⋅3 = 1$.

Por Maria Luiza Alves Rizzo
Professora de Matemática