Retas paralelas

As retas paralelas são retas que estão no mesmo plano e não possuem nenhum ponto em comum, ou seja, retas r e s são paralelas quando não se encontram. Retas paralelas possuem o mesmo sentido e a mesma inclinação, mas ocupam lugares geométricos diferentes em um mesmo plano, o que faz com que elas não possuam nenhum ponto em comum.

Quando classificamos as posições relativas entre duas retas pertencentes a um mesmo plano, encontramos três casos:

• retas concorrentes;

• retas coincidentes;

• retas paralelas.

Com o estudo das retas paralelas, foi possível desenvolver o teorema de Tales e a relação entre a medida dos ângulos formados quando há retas paralelas cortadas por uma transversal. Para dizer que a reta r é paralela à reta s, pode-se utilizar a barra dupla: r//s (lê-se: reta r paralela à reta s).

Leia também: O que é reta?

Tópicos deste artigo

• 1 - Resumo sobre retas paralelas
• 2 - Reta, semirreta e segmento de reta
• 3 - Retas paralelas, perpendiculares, concorrentes e coincidentes
• 4 - Retas paralelas cortadas por uma transversal
  • Videoaula sobre retas paralelas cortadas por uma transversal
• 5 - Teorema de Tales
• 6 - Exercícios resolvidos sobre retas paralelas

Resumo sobre retas paralelas

• Retas paralelas são retas que estão em um mesmo plano e não possuem nenhum ponto em comum.

• Sendo r e s duas retas paralelas, podemos representá-las por r//s.

• Além de retas paralelas, existem retas coincidentes e retas concorrentes.

Reta, semirreta e segmento de reta

Para compreender bem os conceitos envolvendo reta paralela, é importante relembrar os conceitos de semirreta e segmento de reta. O conceito de reta é primitivo, pois sabemos das suas características de forma intuitiva. A reta possui infinitos pontos, e todos esses pontos pertencem a ela, isto é, a reta é infinita para ambas as direções. A partir desse conceito primitivo é que conseguimos definir semirreta.

Uma semirreta ocorre quando limitamos um dos lados da reta. Dessa forma, a semirreta parte de um ponto qualquer e vai até o infinito. Veja um exemplo a seguir:

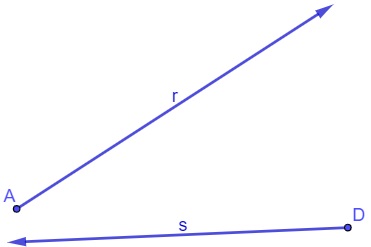
O segmento de reta é uma parte de uma reta. Ele será limitado dos dois lados, ou seja, ele liga dois pontos.

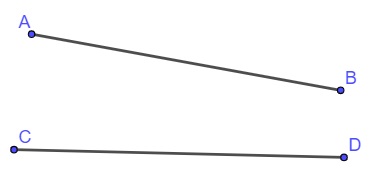
Retas paralelas, perpendiculares, concorrentes e coincidentes

Ao comparar a posição relativa entre duas ou mais retas pertencentes ao mesmo plano, existem três casos possíveis: as retas paralelas, as concorrentes e as coincidentes. As retas podem ser, também, perpendiculares, que é um caso particular de reta concorrente.

• Retas paralelas: considerando duas retas, r e s, ambas são classificadas como paralelas quando não possuem nenhum ponto em comum. Duas retas paralelas são retas que não se cruzam. Para que isso aconteça, as retas têm a mesma inclinação, mas ocupam lugares diferentes em um mesmo plano. Quando r e s são paralelas, elas podem ser representadas por r//s.

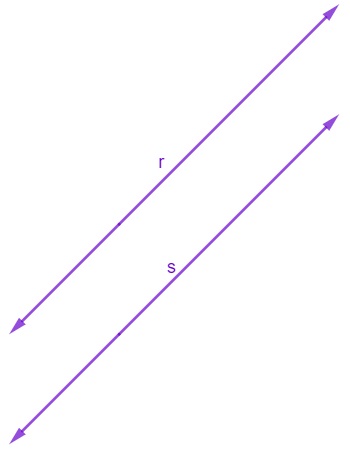
• Retas coincidentes: duas retas são coincidentes quando, na verdade, representam a mesma reta. Retas coincidentes possuem infinitos pontos em comum.

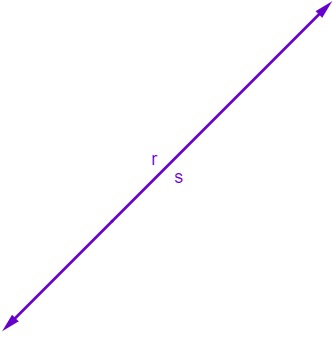
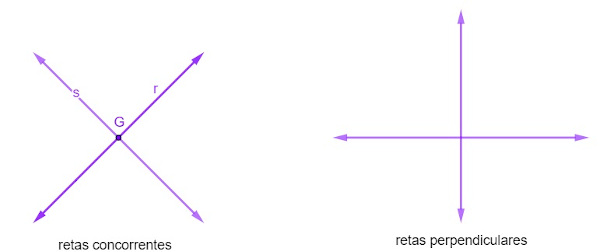
• Retas concorrentes: duas retas são classificadas como concorrentes quando elas possuem um ponto em comum, ou seja, quando elas se encontram em um único ponto. Quando essas retas se cruzam formando um ângulo de 90° entre si, temos um caso particular de retas concorrentes, que são as retas perpendiculares.

Retas paralelas cortadas por uma transversal

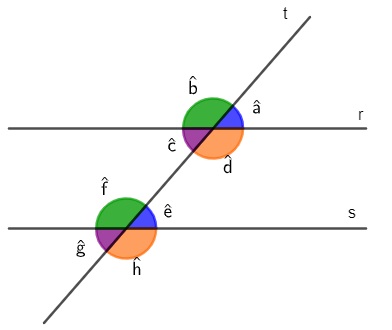
Considera-se como transversal uma reta que corta duas retas paralelas. Quando isso ocorre, é possível verificar a formação de quatro ângulos com cada uma das retas. Ao comparar os ângulos formados, percebe-se uma relação importante entre as retas:

Para se aprofundar no assunto, leia: Retas paralelas cortadas por uma transversal.

• Videoaula sobre retas paralelas cortadas por uma transversal

Teorema de Tales

O teorema de Tales é uma relação importante que pode ser desenvolvida a partir do estudo das retas paralelas. O matemático Tales de Mileto demonstrou uma relação entre os segmentos de reta quando há retas paralelas cortadas por transversais. O enunciado desse teorema diz o seguinte:

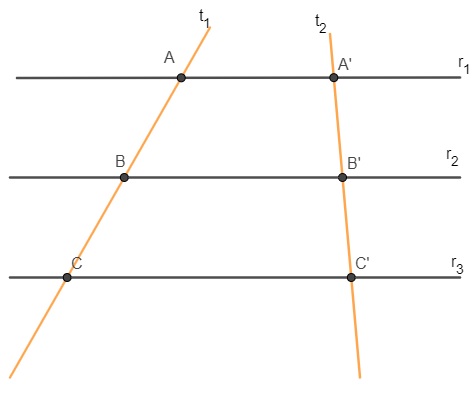
Dessa forma, o teórico demonstrou que os segmentos formados pelas retas transversais são sempre proporcionais, o que torna possível encontrar valores desconhecidos utilizando a seguinte relação:

Leia também: Posição relativa entre reta e plano

Exercícios resolvidos sobre retas paralelas

Questão 1

Considerando duas retas que pertencem ao mesmo plano, podemos afirmar que ambas são paralelas quando

A) elas possuem somente um ponto em comum.

B) elas possuem exatamente dois pontos em comum.

C) elas possuem infinitos pontos em comum.

D) elas não possuem nenhum ponto em comum.

Resolução:

Alternativa D

Retas paralelas não possuem ponto(s) em comum.

Questão 2

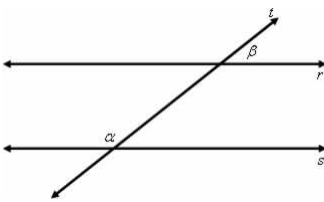
(Itame) Na figura abaixo, as retas r e s são paralelas, cortadas por uma transversal t. Se a medida do ângulo alfa é o triplo da média do ângulo beta, então a diferença entre alfa e beta vale

A) 90°.

B) 85°.

C) 80°.

D) 75°.

Resolução:

Alternativa A

Sabemos que α = 3ꞵ e que um ângulo obtuso e um ângulo agudo, nessa situação, resultam sempre em 180°.

α + ꞵ = 180

3ꞵ + ꞵ = 180

4ꞵ = 180

ꞵ = 180 : 4

ꞵ = 45°

Se ꞵ = 45, então α = 3ꞵ = 3 · 45 = 135°.

Logo, a diferença entre α e ꞵ = 135 – 45 = 90°.

Por Raul Rodrigues de Oliveira
Professor de Matemática