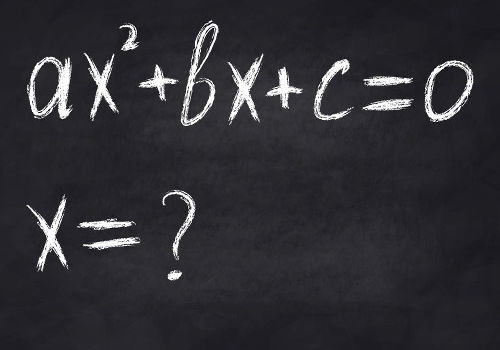
Raízes da função de 2º Grau
Determinar as raízes da função de 2º grau é encontrar os valores de x que tornam uma equação válida.
Para uma experiência de sua escola, um rapaz realiza o lançamento de um peso, que tem seu movimento descrito pela função h(x) = – 2x2 + 50, na qual h(x) é a altura do peso e x sua distância em relação ao rapaz, dada em metros. A que distância do ponto onde foi lançado o peso caiu?
a) 5 metros
b) – 5 metros
c) 10 metros
d) 15 metros
e) 9 metros
A função f(x) = x2 + 8x – 9 é do segundo grau, porque o grau do maior dos monômios que compõe sua regra é 2. Além disso, essa função está escrita na forma f(x) = ax2 + bx + c. Sabendo disso, qual é a soma das raízes da função apresentada acima?
a) 8
b) – 8
c) 1
d) – 9
e) 10
Quais são as raízes da função: f(x) = 2(x – 4)(x + 4)?
a) 0
b) 1 e – 1
c) 2 e – 2
d) 3 e – 3
e) 4 e – 4
A função f(x) = – 3x2 + 12x – 9 é uma função do segundo grau. Das alternativas abaixo, qual é a que resulta da diferença entre as duas raízes da função?
a) 2
b) 3
c) 4
d) 5
e) 6
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)