Uma reta numérica é uma reta comum sobre a qual é estabelecida uma relação biunívoca com o conjunto dos números reais. Essa relação é como uma função bijetora, que relaciona cada ponto da reta a um único número real.
Como a relação é biunívoca (a função é bijetora), todos os pontos da reta estão relacionados a números reais, de modo que cada ponto está ligado a um único número. Ao mesmo tempo, todos os números reais estão relacionados a pontos da reta, de forma que cada número real está ligado a um único ponto da reta. Excluindo-se, é claro, representações distintas para o mesmo número, como 2 e √4.
Portanto, cada número real pode ser compreendido como um “endereço” para um ponto da reta. Isso significa que um número real não nos levaria a dois pontos distintos ou a lugar nenhum.
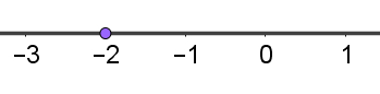
Na reta numérica a seguir, o número – 2 representa o “endereço” do ponto em destaque. Note que a distância entre esse ponto e a origem é 2 un, e que o sentido percorrido para chegar até sua localização é o negativo.
Ao combinar duas retas numéricas para formar o plano cartesiano, criamos a possibilidade de marcar a localização de qualquer ponto nele.
Localização de pontos no plano cartesiano
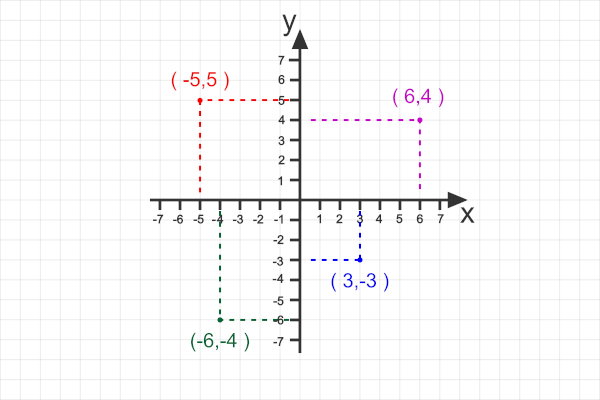
As duas retas numéricas usadas para determinar o plano cartesiano recebem o nome de eixos. A reta horizontal é chamada de eixo x, ou eixo das abscissas, e a reta vertical é chamada de eixo y, ou eixo das ordenadas.
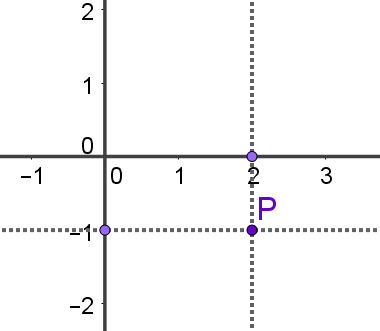
Os pares ordenados são duplas de números usadas para determinar a localização de pontos no plano, por exemplo: P(2, – 1). Esse ponto é composto por uma coordenada referente ao eixo x (a primeira que é igual a 2) e por outra referente ao eixo y: – 1. As coordenadas dos pontos sempre serão apresentadas nessa ordem.
Para marcar esse ponto no plano cartesiano, devemos fazer o seguinte:
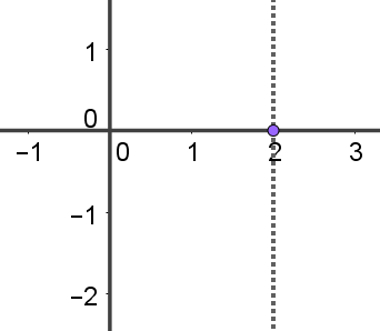
1 – Sabendo que a coordenada x = 2, procuraremos o número 2 sobre o eixo x e faremos nesse ponto uma reta perpendicular a esse eixo. A imagem a seguir mostra essa construção.
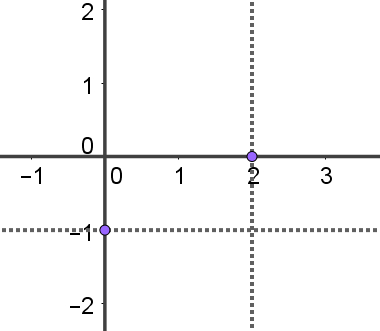
2 – Sabendo que a coordenada y = – 1, procuraremos o número – 1 sobre o eixo y e faremos nesse ponto uma reta perpendicular a esse eixo. A imagem a seguir mostra essa construção, dado que a anterior já havia sido feita.
3 – O ponto de encontro entre as duas retas que foram construídas é o ponto P, ou seja, ele fica localizado aí.
Resultado da criação do plano cartesiano
A partir do plano cartesiano e da localização dos pontos, é possível construir toda a geometria analítica. Esse campo de conhecimento busca estudar a geometria plana e espacial utilizando ferramentas da álgebra. Isso permitiu a demonstração de muitos resultados que ainda não eram possíveis, outras maneiras de demonstrar resultados que já estavam prontos e a criação de muitas propriedades que ainda não haviam sido observadas.
O principal conceito introduzido pela geometria analítica é o de distância entre dois pontos, que é o que dá a base para a construção de diversas figuras geométricas no plano cartesiano e cria mecanismos para demonstrar propriedades que as envolvem.
Dados dois pontos A (xA, yA) e B (xB, yB), a distância entre eles é dada pela seguinte fórmula:
Por Luiz Paulo Moreira
Graduado em Matemática