O dispositivo prático de Briot-Ruffini é uma forma de dividir um polinômio de grau n > 1 por um binômio do 1º grau da forma x – a. Esse método é uma maneira simples de realizar a divisão entre um polinômio e um binômio, uma vez que, para realizar essa operação utilizando a definição, é bastante trabalhoso.
Leia também: O que é um polinômio?
Tópicos deste artigo
Passo a passo da divisão de polinômios pelo método de Briot-Ruffini
Esse dispositivo pode ser utilizado na divisão entre um polinômio P(x) que possui grau n maior que 1 (n >1) e um binômio do tipo (x – a). Vamos acompanhar o passo a passo no exemplo a seguir:
Exemplo
|
Utilizando o dispositivo prático de Briot-Ruffini, divida o polinômio P(x) = 3x3 + 2x2 + x +5 pelo binômio D(x) = x +1. |
Passo 1 – Desenhar dois segmentos de reta, um na horizontal e outro na vertical.

Passo 2 – Colocar os coeficientes do polinômio P(x) no segmento de reta horizontal e à direita do segmento vertical e repetir o primeiro coeficiente na parte de baixo. No lado esquerdo do segmento vertical, devemos colocar a raiz do binômio. Para determinar a raiz de um binômio, basta igualá-lo a zero, assim:
x + 1 = 0
x = – 1
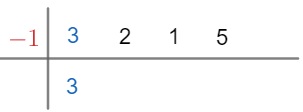
Passo 3 – Vamos multiplicar a raiz do divisor pelo primeiro coeficiente localizado abaixo da linha horizontal e, em seguida, somar o resultado pelo próximo coeficiente localizado acima da linha horizontal. Em seguida, vamos repetir o processo até o último coeficiente, nesse caso o coeficiente 5. Veja:
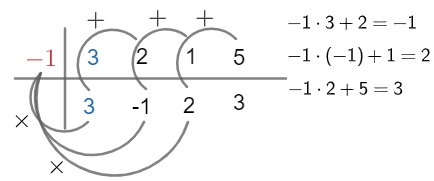
Após realizar esses três passos, vamos analisar o que o algoritmo nos fornece. Na parte superior da linha horizontal e à direita da linha vertical, temos os coeficientes do polinômio P(x), assim:
P(x) = 3x3 + 2x2 + x +5
O número –1 é a raiz do divisor e, portanto, o divisor é D(x) = x + 1. Por fim, o quociente pode ser encontrado com os números localizados abaixo da linha horizontal, sendo o último número o resto da divisão.
Lembre-se de que o grau do dividendo é 3 e o grau do divisor é 1, portanto o grau do quociente é dado por 3 – 1 = 2. Assim, o quociente é:
Q(x) = 3x2 – 1x + 2
Q(x) = 3x2 – x + 2
Observe novamente que os coeficientes (assinalados em verde) são obtidos com os números abaixo da linha horizontal e que o resto da divisão é: R(x) = 3.
Utilizando o algoritmo da divisão, temos que:
Dividendo = Divisor · Quociente + Resto
3x3 + 2x2 + x +5 = (x + 1) · (3x2 – x + 2) + 3
Exercícios resolvidos
Questão 1 – (Furg) Na divisão de um polinômio P(x) pelo binômio (x – a), ao se usar o dispositivo prático de Briot-Ruffini, encontrou-se:

Os valores de a, q, p e r são, respectivamente:
a) – 2; 1; – 6 e 6.
b) – 2; 1; – 2 e – 6.
c) 2; – 2; – 2 e – 6.
d) 2; – 2; 1 e 6.
e) 2; 1; – 4 e 4.
Solução:
Observe que o enunciado afirma que o polinômio P(x) foi dividido pelo binômio (x – a), logo ele será o divisor. Do dispositivo prático de Briot-Ruffini, temos que o número à esquerda da linha vertical é a raiz do divisor, assim a = – 2.
Ainda com base no dispositivo prático de Briot-Ruffini, sabemos que é necessário repetir o primeiro coeficiente do dividendo abaixo da linha horizontal, logo q = 1.
Para determinar o valor de p, vamos utilizar novamente o dispositivo prático. Veja:
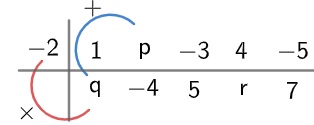
– 2 · q + p = – 4
Sabemos que q = 1, descoberto anteriormente, assim:
– 2 · 1 + p = – 4
– 2 + p = – 4
p = – 4 + 2
p = –2
De maneira análoga, temos que:
– 2 · 5 +4 = r
– 10 + 4 = r
r = – 6
Portanto, a = – 2; q = 1; p = –2; r = – 6.
Resposta: alternativa b.
Leia também: Divisão de polinômios – dicas, métodos, exercícios
Questão 2 – Divida o polinômio P(x) = x4 – 1 pelo binômio D(x) = x – 1.
Solução:
Observe que o polinômio P(x) não está escrito em sua forma completa,. Antes de aplicarmos o dispositivo prático de Briot-Ruffini, devemos escrevê-lo em sua forma completa. Veja:
P(x) = x4 + 0x3 + 0x2 + 0x – 1
Feita essa observação, podemos dar continuidade ao dispositivo prático de Briot-Ruffini. Vamos determinar a raiz do divisor e, em seguida, aplicar o algoritmo:
x – 1 = 0
x = 1
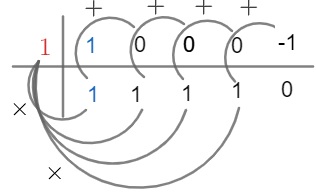
Podemos concluir que, ao dividir o polinômio P(x) = x4 – 1 pelo binômio D(x) = x – 1, temos o seguinte: polinômio Q(x) = x3 + x2 + x + 1 e resto R(x) = 0.
Por Robson Luiz
Professor de Matemática

