Operações com vetores são as operações algébricas feitas com vetores. Os vetores são instrumentos matemáticos de representação das grandezas vetoriais, possuindo módulo, direção e sentido. Com eles pode-se realizar diversas operações algébricas, como adição, subtração e multiplicação.
Leia também: Grandezas vetoriais e escalares — quais as diferenças entre elas?
Tópicos deste artigo
- 1 - Resumo sobre operações com vetores
- 2 - O que são vetores?
- 3 - Operações com vetores
- 4 - Exercícios resolvidos sobre operações com vetores
Resumo sobre operações com vetores
-
Os vetores simbolizam as grandezas vetoriais caracterizando-as em módulo, direção e sentido.
-
Há várias operações algébricas que se pode fazer com vetores, como adição, subtração e multiplicação de um número real por um vetor.
-
Para vetores em uma mesma direção, pode-se realizar as operações de adição ou subtração.
-
A adição de vetores em uma mesma direção consiste na soma do módulo dos vetores.
-
A subtração de vetores na mesma direção (obrigatoriamente com vetores em sentidos opostos) é o mesmo que diminuir os módulos dos vetores, a fim de encontrar o vetor resultante, que terá a mesma direção dos vetores envolvidos na operação, mas seu sentido será igual ao do maior vetor.
Não pare agora... Tem mais depois da publicidade ;) -
A adição entre vetores perpendiculares é resolvida pelo teorema de Pitágoras.
-
A adição entre vetores oblíquos é resolvida pela lei dos cossenos e a regra do paralelogramo.
-
A multiplicação de um vetor por um número real é a operação em que se utiliza um número real e se faz seu produto com um vetor.
-
Para decompor os vetores, basta “quebrá-los” em duas componentes, uma horizontal e outra vertical.
O que são vetores?
Os vetores são representados por segmentos de retas em formato de seta e têm como função caracterizar as grandezas físicas vetoriais com módulo, direção e sentido.
-
Módulo: também chamado por valor numérico, norma, intensidade ou tamanho da grandeza vetorial, é representado por \(\left|\vec{v}\right| \) ou v.
Não pare agora... Tem mais depois da publicidade ;)
-
Direção: informa para onde o vetor está virado, pode ser horizontal, vertical ou diagonal.
-
Sentido: informa para onde o vetor está apontado, pode ser à direita, à esquerda, para cima, para baixo, a leste, a norte, a sul, a oeste, entre outros.
→ Videoaula sobre vetores
Operações com vetores
Pode-se realizar diversas operações algébricas envolvendo vetores, como adição, subtração e produto, sendo importante destacar que o vetor que resulta dessas operações é chamado de resultante. Para descobrí-lo, considera-se os módulos, direções e sentidos dos vetores envolvidos nas operações.
→ Soma e subtração de vetores na mesma direção
Quando os vetores estão na mesma direção, é possível realizar tanto a soma quanto a subtração deles. Veja a seguir.
▪ Soma de vetores na mesma direção
Na soma de vetores na mesma direção, é necessário que ambos os vetores estejam em um mesmo sentido, assim, o vetor resultante será resultado da adição dos módulos dos vetores envolvidos e terá a mesma direção e sentido deles.
▪ Subtração de vetores na mesma direção
Na subtração de vetores na mesma direção, eles devem ter sentidos opostos. O vetor resultante da operação será resultado da diminuição dos módulos dos vetores envolvidos, terá a mesma direção deles, mas seu sentido será o mesmo do vetor com maior tamanho.
Exemplo:
Dados um vetor \(\vec{v}\), com tamanho de 2 unidades no sentido à direita, e outro vetor, \(-\vec{u}\), com tamanho de 4 unidades no sentido à direita, qual será o vetor resultante da subtração entre eles?
Resolução:
Antes de tudo, vale falar que os vetores representados com um menos (–) na frente, como \(-\vec{u}\), estão no sentido oposto ao retratatado, então, no enunciado, ele é representado por:
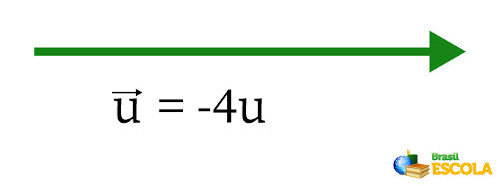
Também é o mesmo que dizer que ele vale:
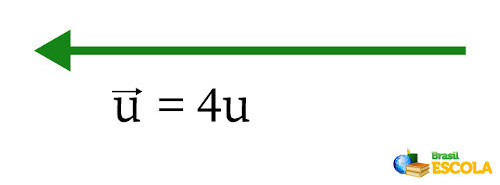
Só assim se consegue fazer a subtração entre eles:
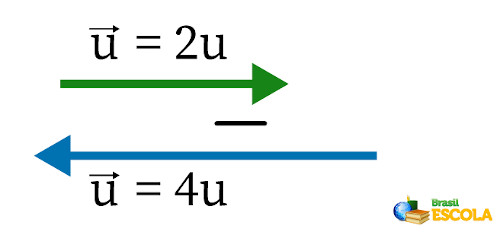
Simultaneamente, na subtração dos vetores, encontra-se a sua direção. Para isso, basta colocar um abaixo do outro, e o vetor resultante é o que falta para completar o vetor azul \(\vec{u}\).
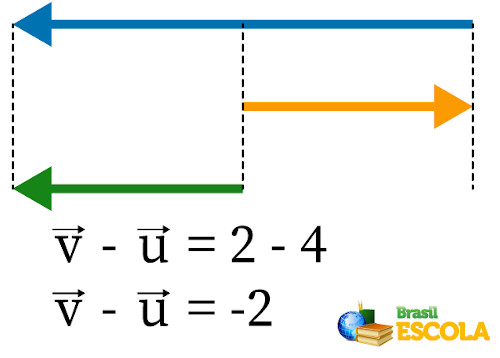
Então a subtração entre os dois vetores é –2, o que significa dizer que o vetor resultante possui sentido contrário ao vetor verde \(\vec{v}\) e módulo de 2 unidades, com sentido para a esquerda e direção horizontal.
→ Soma e subtração de vetores perpendiculares
Com vetores perpendiculares entre si, ou seja, formando um ângulo de 90° entre eles, não ocorre a subtração, o que se vê é a representação de um vetor com sinal negativo, como \(-\vec{v}\), significando que ele está em seu sentido oposto.
Para resolver esse problema, faz-se como demonstrado no exemplo anterior: muda-se o sentido, tornando-se seu módulo positivo. Assim, para vetores perpendiculares, tem-se sempre a operação de soma, em que se usa o teorema de Pitágoras, cuja fórmula é:
\({hipotenusa}^2={{cateto}_1}^2+{{cateto}_2}^2\)
Exemplo:
Dados um vetor \(\vec{v}\) com módulo de 1 unidade e orientação vertical para cima e outro vetor \(\vec{v}\) com módulo de 5 unidades e orientação horizontal para direita, qual será o vetor resultante da soma entre eles?
Resolução:
Primeiramente se desenha os vetores:
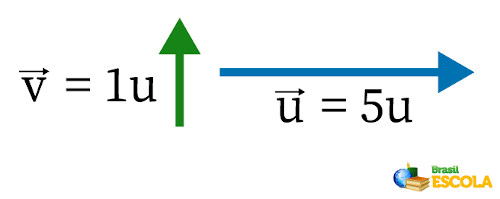
Posteriormente, encontra-se o vetor resultante. Para isso, seus vetores são movimentados sem modificar seus tamanhos até que eles se encontrem, e pontilhados de mesmo tamanho são traçados, formando um quadrado. Em seguida, faz-se uma linha diagonal que representa o vetor resultante \(\vec{R} \) da soma entre esses dois vetores, como abaixo:
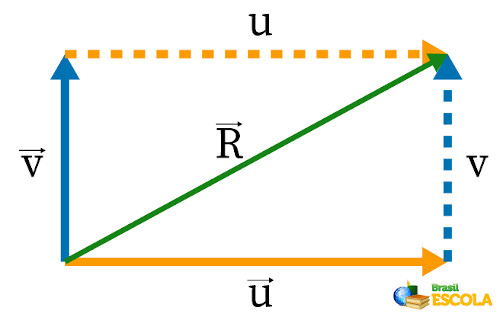
Como já foram encontrados o sentido e a direção do vetor resultante, nordeste e diagonal, respectivamente, então, por meio do teorema de Pitágoras, encontra-se seu módulo:
\({hipotenusa}^2={{cateto}_1}^2+{{cateto}_2}^2\)
A hipotenusa equivale ao módulo do vetor resultante \(\vec{R}\) e os catetos são os módulos dos vetores envolvidos:
\(R^2=u^2+v^2\)
\(R^2=1^2+5^2\)
\(R^2=1+25\)
\(R^2=26\)
\(R=\sqrt{26\ u}\)
\(R\approx5,09\ u\)
O módulo do vetor resultante é de 5,09 unidades.
Saiba mais: Quais são as aplicações do teorema de Pitágoras?
→ Soma e subtração de vetores oblíquos
Com vetores oblíquos entre si, ou seja, formando um ângulo diferente de 0°, 90° e 180° entre eles, a subtração é a representação do sentido oposto. Ela será feita da mesma forma como já foi retratado, então há também sempre a operação de adição.
Para encontrar o sentido e direção do vetor resultante da operação, usa-se a regra do paralelogramo, e para descobrir seu módulo, a lei dos cossenos, cuja fórmula é:
\({hipotenusa}^2={{cateto}_1}^2+{{cateto}_2}^2-2\bullet{cateto}_1\bullet{cateto}_2\bullet\cos{\theta}\)
Exemplo:
Dados um vetor \(\vec{v}\) com módulo de 3 unidades e orientação a nordeste e outro vetor \(\vec{u} \) com módulo de 4 unidades e orientação a sudeste, qual será o vetor resultante da soma entre eles, sabendo que o ângulo formado pela sua combinação é de 60°?
Resolução:
Primeiramente se desenha os vetores:
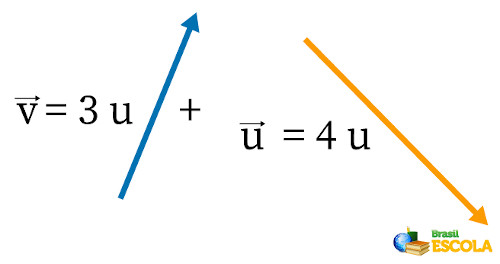
Usando a regra do paralelogramo, é possível descobrir a orientação do vetor resultante. Essa regra se trata de movimentar os vetores sem modificar seus tamanhos até seu encontro e traçar pontilhados de mesmo tamanho, formando um quadrado. Em vetores perpendiculares, forma-se um paralelogramo em vez de um quadrado. Depois se faz uma linha diagonal, representando o vetor resultante \(\vec{R}\) da soma entre esses dois vetores, como representado abaixo:
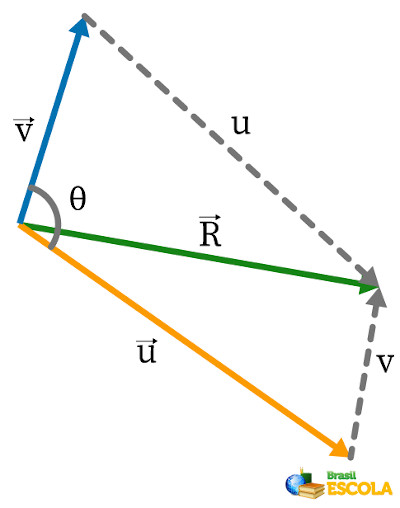
O vetor resultante possui sentido para direita e direção diagonal. Então, calculando o seu módulo com base na lei dos cossenos, tem-se:
\({hipotenusa}^2={{cateto}_1}^2+{{cateto}_2}^2-2\bullet{cateto}_1\bullet{cateto}_2\bullet\cos{\theta}\)
A hipotenusa equivale ao módulo do vetor resultante \(\vec{R} \) e os catetos são os módulos dos vetores envolvidos:
\(R^2=u^2+v^2-2\bullet u\bullet v\bullet\cos{\theta}\)
\(R^2=4^2+3^2-2\bullet4\bullet3\bullet\cos60°\)
\(R^2=16+9-24\bullet0,5\)
\(R^2=16+9-12\)
\(R^2=13\)
\(R=\sqrt{13}\)\(R\approx3,6\ u\)R≈3,6 u
O módulo do vetor resultante é de 3,6 unidades.
→ Multiplicação de um vetor por um número real
A multiplicação de um vetor por um número real resultará em um novo vetor de mesma direção, mas que poderá ter um novo sentido, dependendo do sinal do número real. Se ele for positivo, então o sentido será o mesmo, já se for negativo, então o sentido será contrário, e seu módulo será o produto entre o número n e o vetor \(\vec{v}\).
\(v_{novo}=n\bullet\vec{v}\)
Exemplo:
Dado um vetor \(\vec{v}\) com módulo de 10 unidades e orientação a sudeste, qual será seu valor se ele for multiplicado pelo número real 50?
Resolução:
A direção e o sentido não mudarão (diagonal e a noroeste respectivamente), mas seu módulo mudará e terá valor igual a:
\(v_{novo}=n\bullet\vec{v}\)
\(v_{novo}=50\bullet10\)
\(v_{novo}=500\ u\)
O módulo ou tamanho do vetor novo é de 500 unidades.
Decomposição de vetores
A decomposição de vetores é uma ferramenta utilizada para encontrar as componentes x e y de algum vetor. Faz-se como se fosse o processo inverso ao da soma de vetores, já que serão encontrados os vetores que se somaram, resultando no vetor resultante.
Se se tem um vetor \(\vec{v}\) inclinado e se quer encontrar sua decomposição vetorial, basta desenhar da seguinte forma:
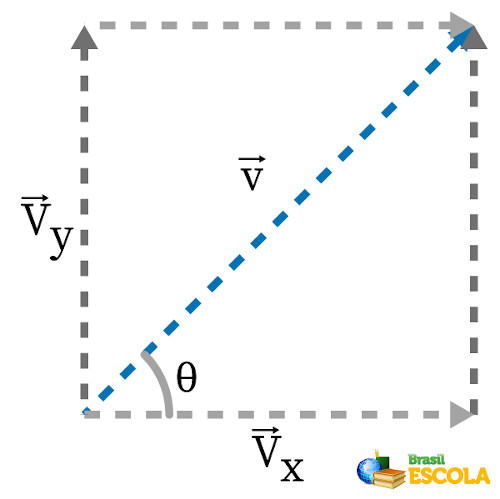
Em que \(\vec{v}\) é o vetor resultante da soma vetorial entre \(\vec{v_x}\ \) e \(\vec{v_y}\). No desenho, pode-se observar a formação de um triângulo retângulo, como a seguir:
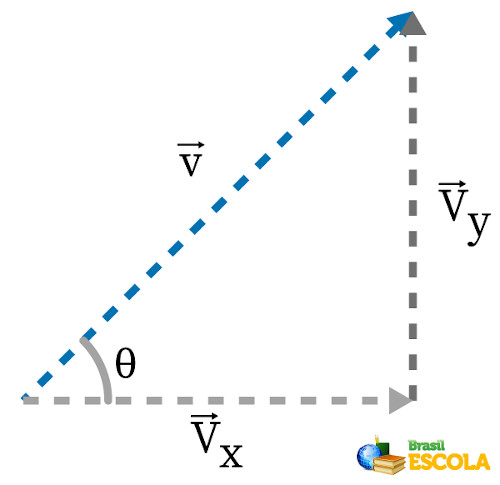
Assim, é possível encontrar os módulos das componentes \(\vec{v_x}\) e \(\vec{v_y}\) usando as relações trigonométricas do triângulo retângulo. Descobrindo \({\ v}_y\):
\(\sin{\theta=\frac{cateto\ oposto}{hipotenusa}}\)
\(\sin{\theta=\frac{v_y}{v}}\)
\(v\bullet\sin{\theta=v_y}\)
Descobrindo \(v_x\):
\(\cos{\theta=\frac{cateto\ adjacente}{hipotenusa}}\)
\(\cos{\theta=\frac{v_x}{v}}\)
\(v\bullet\cos{\theta=v_x}\)
Exemplo:
Realizando uma força para puxar um bloco no chão, com o módulo da força sendo de 100 N e tendo inclinação de 30° com a horizontal, quais serão as componentes horizontal e vertical dessa força?
Resolução:
Primeiramente, faz-se o desenho da força e de suas componentes:
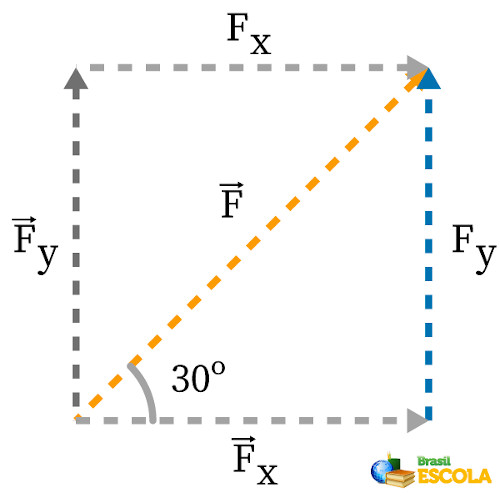
Calculando o módulo da componente horizontal \(F_x\):
\(F_x=F\bullet\cos60°\)
\(F_x=100\bullet\frac{\sqrt3}{2}\)
\(F_x=50\sqrt3\ N\)
Calculando o módulo da componente vertical \(F_y\):
\(F_y=F\bullet\sin60°\)
\(F_y=100\bullet0,5\)
\(F_y=50\ N\)
Saiba também: Operações com frações — quais são e como fazer?
Exercícios resolvidos sobre operações com vetores
Questão 1
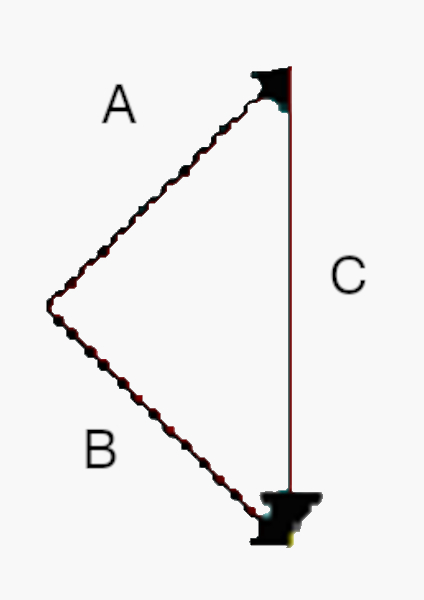
Os vetores \(\vec{a}\), \(\vec{b}\) e \(\vec{c}\) têm módulos iguais a 4, 8 e 12 respectivamente. Quais os módulo do vetor \(\vec{s}=\vec{a}+\vec{b}\) e do vetor \(\vec{v}=\vec{s}+\vec{c}\)?
A) 12, 12
B) 12, 24
C) 24, 18
D) 0, 24
E) 24, 12
Resolução:
Alternativa B
O módulo do vetor \(\vec{s}\) é a soma dos vetores \(\vec{a}\) e \(\vec{b}\), então:
\(\vec{s}=\vec{a}+\vec{b}\)
\(\vec{s}=4+8\)
\(\vec{s}=12\)
Já o módulo do vetor \(\vec{v}\) é a soma dos vetores \(\vec{s}\) e \(\vec{c}\), então:
\(\vec{v}=\vec{s}+\vec{c}\)
\(\vec{v}=12+12\)
\(\vec{v}=24\)
Questão 2
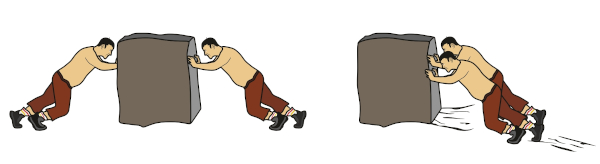
(Enem) A força de atrito é uma força que depende do contato entre corpos. Pode ser definida como uma força de oposição à tendência de deslocamento dos corpos e é gerada devido a irregularidades entre duas superfícies em contato. Na figura, as setas representam forças que atuam no corpo e o ponto ampliado representa as irregularidades que existem entre as duas superfícies.
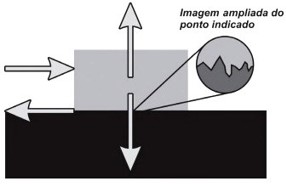
Na figura, os vetores que representam as forças que provocam o deslocamento e o atrito são, respectivamente:
A) ![]()
B) 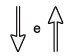
C) ![]()
D) 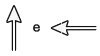
E) 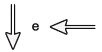
Resolução:
Alternativa A
Como o movimento é feito na direção horizontal, o par ação e reação possui sentido oposto.
Por Pâmella Raphaella Melo
Professora de Física