Grandezas vetoriais e escalares

Grandezas vetoriais e grandezas escalares são tipos de grandezas físicas que dependem de diferentes informações para serem definidas. Para as grandezas escalares, é necessário que se conheçam seu módulo (ou norma) e a unidade de medida. Para as grandezas vetoriais, é preciso conhecer, além do módulo e unidade medida, sua direção e sentido.

A Física está repleta de grandezas vetoriais e escalares. Para saber identificar cada uma delas, é preciso entender aquilo que as define, portanto saber quais são as características das grandezas escalares e vetoriais, conhecer a diferença entre grandezas fundamentais e derivadas e comparar grandezas direta e inversamente proporcionais. Esse conhecimento perpassa todos os conteúdos da Física, sendo, portanto, de grande utilidade para o estudo dessa área do conhecimento.

Leia também: O que é grandeza?

Tópicos deste artigo

• 1 - Diferenças entre grandezas escalares e vetoriais
• 2 - Grandezas físicas
• 3 - Grandezas e medidas
• 4 - Grandezas direta e inversamente proporcionais

Diferenças entre grandezas escalares e vetoriais

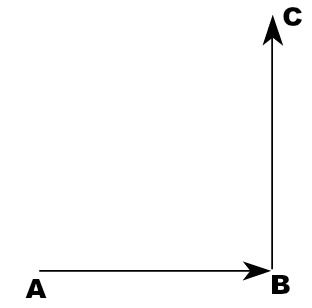
Todas as grandezas físicas podem ser classificadas em dois tipos: as grandezas escalares e as vetoriais. A diferença mais básica entre esses dois tipos de grandezas é que as escalares podem ser representadas de forma satisfatória por intermédio apenas do número e de uma unidade de medida. Em contrapartida, as grandezas vetoriais precisam ser expressas com base em mais informações, como o seu valor numérico, direção e sentido, além de uma unidade de medida.

→ Grandezas escalares

Grandezas escalares são aquelas que podem ser escritas na forma de um número, seguido de uma unidade de medida. Em outras palavras, elas são completamente definidas se soubermos o seu valor, também chamado de módulo, e a forma como ela é medida.

São exemplos de grandezas escalares o comprimento, o tempo, a temperatura e a massa. Confira algumas formas como essas grandezas podem ser expressas:

• 1 m – um metro; 10 cm – dez centímetros; 2 mm – dois milímetros.
• 10 s – dez segundos; 15 min – quinze minutos; 1 h – uma hora.
• 25º C – vinte e cinco graus Celsius; 86º F – oitenta e seis graus Fahrenheit; 10 K – dez kelvin.
• 200 g – duzentos gramas; 10 mg – dez miligramas; 2 kg – dois quilogramas.

Resumindo:

Veja também: Tudo o que você precisa saber sobre a Física Mecânica que cai no Enem

→ Grandezas vetoriais

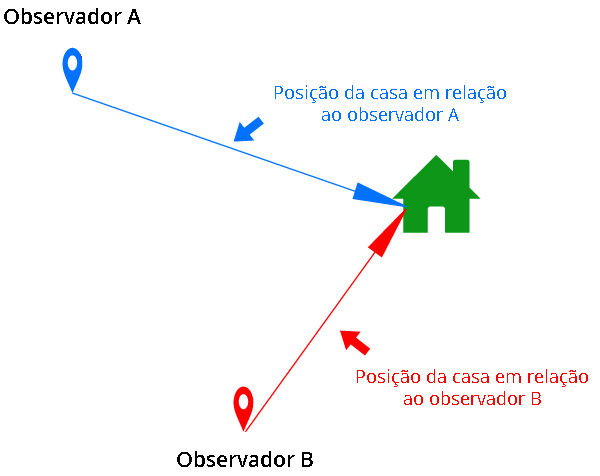
Grandezas vetoriais precisam ser expressas por um número (módulo), uma direção, um sentido e uma unidade de medida. Isso equivale a dizer que essas grandezas podem ser expressas por meio de uma seta (vetor), ou seja, para defini-las, é necessário levar em conta o ponto de vista do observador.

Antes de continuarmos a discutir o que são as grandezas vetoriais, é preciso compreender a diferença entre módulo, direção e sentido:

• Módulo: medida ou o tamanho do vetor que representa a grandeza vetorial.
• Direção: dimensão do espaço que depende do sistema de orientação que é usado. Existem direções tais como largura, altura e profundidade, ou ainda a direção horizontal e vertical, ou direção x, y e z (usadas no sistema cartesiano), ou até mesmo direção leste-oeste, norte-sul.
• Sentido: a orientação se é para cima ou para baixo, para direita ou para esquerda, positivo ou negativo, leste ou oeste, norte ou sul. Toda direção apresenta dois sentidos, que são como a ponta da seta de cada vetor.

Confira alguns exemplos de grandezas vetoriais:

• Posição
• Deslocamento
• Velocidade
• Força
• Aceleração

Além de serem grandezas vetoriais, o que há de comum em todas essas grandezas listadas acima? Todas dependem de uma direção e um sentido. Por exemplo, se alguém lhe pergunta onde fica a padaria, não basta responder que ela fica a 50 m de distância, é necessário que se estabeleça algum sistema de referência, como o seguinte:

Para chegar à padaria, vire à direita (sentido) a partir daqui (origem do sistema de referência) e mova-se em linha reta (direção), percorrendo 50 m (módulo e unidade de medida).

Resumindo:

Leia também: Operações com vetores

Grandezas físicas

Já que estamos tratando das grandezas vetoriais e escalares, é pertinente entender o que é uma grandeza física. Grandezas físicas são todas as características inerentes a um corpo ou a um tipo qualquer de fenômeno que possa ser medido. A partir de um conjunto básico de grandezas físicas, conhecido como grandezas fundamentais, é possível expressar todas as demais grandezas. Além disso, para serem expressas de forma quantitativa, ou seja, em números, as grandezas físicas devem ser definidas a partir de um sistema de medidas. Atualmente, o sistema de medidas usado pela comunidade científica e em quase todo o mundo é o Sistema Internacional de Unidades, também conhecido com SI.

Se quiser entender mais profundamente sobre como funcionam as grandezas, sugerimos que acesse o nosso texto – com conteúdo um pouco mais avançado – sobre a análise dimensional, que é uma ferramenta usada para o estudo das grandezas físicas.

Grandezas e medidas

As grandezas físicas fundamentais, bem como suas medidas, são mostradas na tabela abaixo. Nessa tabela você encontrará tais grandezas organizadas de acordo com seu nome e seu símbolo, conforme o SI. Confira:

A partir das grandezas mostradas acima, são definidas centenas de outras grandezas derivadas, que são escritas por meio da combinação de grandezas fundamentais, como a velocidade, que é uma combinação entre as grandezas comprimento e tempo:

Confira alguns exemplos de grandezas derivadas e suas unidades de medida:

• Aceleração – [m].[s]^-2
• Força – [kg]. [m].[s]^-2
• Densidade – [kg].[m]^-³
• Pressão – [kg]. [m]^-1.[s]^-2

Grandezas direta e inversamente proporcionais

Ao falar de grandezas, também é válido analisar a questão da proporcionalidade entre elas. Grandezas proporcionais são aquelas que aumentam uma em função da outra. Quanto maior for a distância percorrida por um móvel em um certo intervalo de tempo, por exemplo, maior será sua velocidade, por isso velocidade e distância percorrida são grandezas diretamente proporcionais. Em contrapartida, quanto maior for o tempo necessário para esse móvel percorrer uma certa distância, menor será sua velocidade, dessa maneira, dizemos que velocidade e tempo são grandezas inversamente proporcionais.

Para definirmos se duas grandezas são proporcionais ou inversamente proporcionais entre si, utilizamos o símbolo α, assim como mostramos no exemplo a seguir:

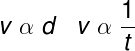
Por Rafael Helerbrock
Professor de Física