O que é lei dos cossenos?

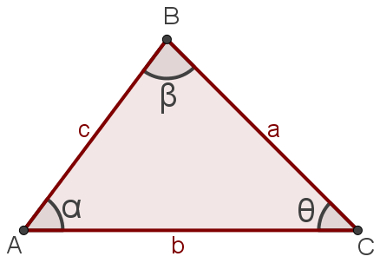
A lei dos cossenos é uma relação trigonométrica usada para relacionar lados e ângulos de um triângulo qualquer, isto é, aquele triângulo que não possui, necessariamente, um ângulo reto. Observe o seguinte triângulo ABC com as medidas em destaque:

A lei dos cossenos pode ser dada por uma das seguintes expressões:

a² = b² + c² – 2·b·c·cosα

b² = a² + c² – 2·a·c·cosβ

c² = b² + a² – 2·b·a·cosθ

Observação: Não é necessário decorar essas três fórmulas. Basta saber que a lei dos cossenos sempre pode ser construída. Observe, na primeira expressão, que o α é o ângulo oposto ao lado cuja medida é dada por a. Começamos a fórmula pelo quadrado do lado oposto ao ângulo que será usado nos cálculos. Ele será igual à soma dos quadrados dos outros dois lados, menos duas vezes o produto dos dois lados que não são opostos a esse ângulo pelo cosseno de α.

Dessa maneira, as três fórmulas acima podem ser reduzidas a:

a² = b² + c² – 2·b·c·cosα

Desde que saibamos que “a” é a medida do lado oposto a “α”, e que “b” e “c” são as medidas dos outros dois lados do triângulo.

Demonstração

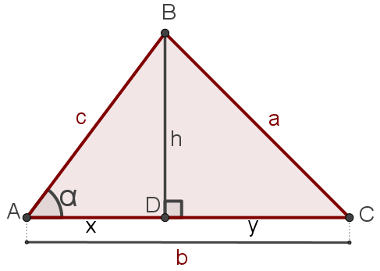
Dado o triângulo ABC qualquer, com as medidas em destaque na seguinte figura:

Considere os triângulos ABD e BCD formados pela altura BD do triângulo ABC. Usando o teorema de Pitágoras em ABD, teremos:

c² = x² + h²

h² = c² – x²

Usando o mesmo teorema para o triângulo BCD, teremos:

a² = y² + h²

h² = a² – y²

Sabendo que h² = c² – x², teremos:

c² – x² = a² – y²

c² – x² + y² = a²

a² = c² – x² + y²

Observe na figura do triângulo que b = x + y, em que y = b – x. Substituindo esse valor no resultado obtido antes, teremos:

a² = c² – x² + y²

a² = c² – x² + (b – x)²

a² = c² – x² + b² – 2bx + x²

a² = c² + b² – 2bx

Ainda observando a figura, perceba que:

cosα = x
            c

c·cosα = x

x = c·cosα

Substituindo esse resultado na expressão anterior, teremos:

a² = c² + b² – 2bx

a² = c² + b² – 2b·c·cosα

Essa é exatamente a primeira das três expressões apresentadas antes. As outras duas podem ser obtidas de maneira análoga a essa.

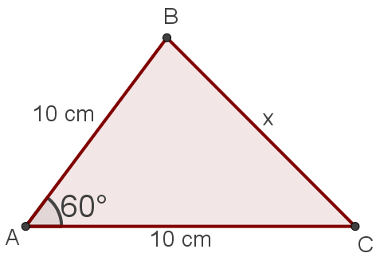
Exemplo – No triângulo a seguir, calcule a medida de x.

Solução:

Usando a lei dos cossenos, perceba que x é a medida do lado oposto ao ângulo de 60°. Sendo assim, o primeiro “número” a aparecer na solução deve ser ele:

x² = 10² + 10² – 2·10·10·cos60°

x² = 100 + 100 – 2·100·cos60°

x² = 200 – 200·cos60°

x² = 200 – 200·1
                          2

x² = 200 – 100

x² = 100

x = ± √100

x = ± 10

Como não existem comprimentos negativos, o resultado deve ser apenas o valor positivo, isto é, x = 10 cm.

Por Luiz Moreira
Graduado em Matemática