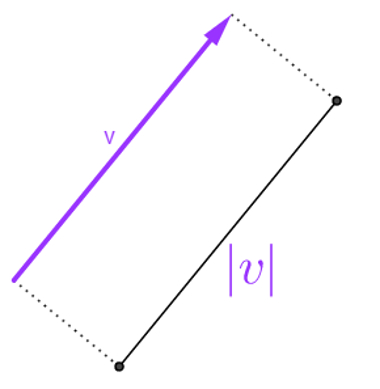
Norma de um vetor

Norma de um vetor é outro nome dado ao módulo de um vetor. Para compreender o conceito de módulo ou norma de um vetor, é importante compreender primeiro o conceito de módulo de um número real, pois ambos se referem ao mesmo procedimento, mas com cálculos diferentes.

Existe uma correspondência entre os números reais e a reta numérica chamada de biunívoca. Isso quer dizer que cada ponto da reta numérica representa um número real e cada número real representa um ponto da reta numérica. Além disso, essa reta é ordenada, ou seja, os números são organizados nela de forma crescente e da direita para a esquerda.

Essas duas características da reta numérica permitem que as distâncias entre números reais sejam calculadas. Portanto, o módulo entre dois números reais x e y fica definido como o valor absoluto da diferença entre x e y e é denotado por |x – y|. Dessa forma, o módulo representa a distância entre dois números reais na reta numérica.

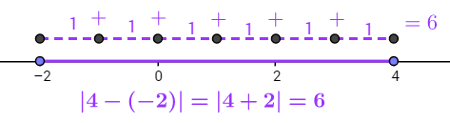
Módulo entre os números reais – 2 e + 4

Observe que a definição acima é para o módulo entre dois números reais. Quando se trata do módulo de um número real, refere-se à distância entre esse número e 0 (zero), que é a origem da reta numérica. Portanto, |x| é a distância entre o ponto x e o ponto 0 em uma reta numérica.

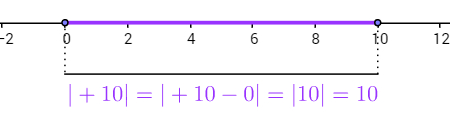
Módulo do número real +10

Em relação aos vetores, eles são objetos matemáticos definidos em qualquer tipo de espaço, seja ele uma reta, seja um plano ou espaços com muitas dimensões. Além disso, são segmentos de reta orientados criados para descrever movimentos retilíneos e possuem marcação de direção, sentido e intensidade. Como se trata de segmentos de reta antes de tudo, é possível medir seus comprimentos utilizando cálculos que envolvem distância entre dois pontos.

Norma de um vetor

→ Primeiro caso:

Tomando o plano como exemplo, geralmente, vetores são representados partindo do ponto O = (0,0) e terminando no ponto A = (x,y). Se esse for o caso do vetor v, pode-se escrever que o vetor v = (x,y). Nesse caso, para calcular o módulo do vetor v, também chamado de norma, basta calcular seu comprimento, obtido pela distância entre os pontos A e O.

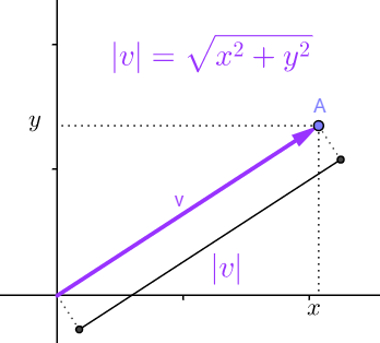
Distância de A até O no plano

→ Segundo caso:

Tomando o plano como exemplo, um vetor pode ter sido obtido em qualquer parte desse plano. Portanto, considerando que o vetor v tenha seu início no ponto G = (a,b) e finde no ponto L = (c,d), a norma desse vetor pode ser obtida de duas formas:

1 – transportando o vetor, sem qualquer rotação ou dilatação, para a origem do plano e repetindo o procedimento anterior.

2 – Calculando a distância entre L e G.

Esse último caso é dado pela seguinte expressão:

Expressão usada para calcular a norma de um vetor qualquer do plano

Por Luiz Paulo Moreira
Graduado em Matemática