Análise dimensional

A análise dimensional é uma ferramenta que possibilita a previsão, inspeção e adaptação das unidades físicas que são utilizadas para a resolução de equações. Na análise dimensional, aplicamos os fundamentos da álgebra a fim de determinarmos em qual unidade de medida alguma grandeza deve ser expressa, de forma a garantir a homogeneidade entre as grandezas.

Tópicos deste artigo

• 1 - Passo a passo da análise dimensional
• 2 - Análise dimensional de fórmulas
• 3 - Conversão de unidades por meio da análise dimensional
• 4 - Análise dimensional no Enem
• 5 - Exercícios resolvidos

Passo a passo da análise dimensional

Usando a análise dimensional, é possível prevermos qual será a unidade de medida de alguma grandeza física que esteja relacionada à resolução de algum problema. Para tanto, é necessário que conheçamos ao menos as unidades fundamentais da Física, listadas no Sistema Internacional de Unidades (SI).

A partir das grandezas fundamentais, como o metro, o quilograma, o segundo e outras, podemos escrever todas as demais grandezas derivadas. A tabela a seguir mostra algumas das mais importantes unidades do SI – é importante conhecê-las, confira:

Análise dimensional de fórmulas

Vamos aprender a fazer a análise dimensional de uma fórmula simples, como a da velocidade média. A velocidade média é calculada pela razão do deslocamento (ΔS) pelo intervalo de tempo (Δt).

Conhecendo as unidades fundamentais do SI, é possível identificar que o deslocamento deve ser medido em metros (m), enquanto o intervalo de tempo deve ser medido em segundos (s). Dessa forma, a unidade de medida de velocidade deve ser dada em metros por segundo (m/s), confira a figura abaixo:

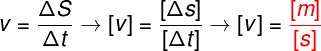
Veja também: Confira exercícios resolvidos sobre o movimento uniforme

Na análise dimensional, realizada anteriormente, perceba que foi necessário conhecermos previamente as unidades de distância e tempo, para que então pudéssemos prever qual deveria ser a unidade de velocidade. Além disso, como a fórmula indicava que as grandezas de distância e tempo estavam divididas uma pela outra, suas unidades também foram divididas.

Algumas fórmulas ou grandezas podem ser um pouco mais trabalhosas para determinarmos as suas unidades, confira um exemplo em que é necessário que conheçamos além das unidades, as fórmulas que permitem calcular as grandezas que estão nelas relacionadas. Confira a seguir o exemplo da fórmula de pressão, no qual queremos determinar qual é a unidade de P:

Para encontrarmos a unidade na qual a pressão deve ser escrita, de acordo com o SI, primeiramente foi necessário que conhecêssemos a sua fórmula. Depois disso, precisaríamos saber em qual unidade a grandeza força é expressa e caso não soubéssemos, seria necessário conhecermos a sua fórmula (F=ma), para encontrarmos a sua unidade.

Feito isso, foi necessário lembrarmos que áreas são medidas em m². Com essas unidades em mãos, voltamos para a fórmula e substituímos cada grandeza com suas respectivas unidades e aplicamos as regras da álgebra: fazemos divisões e multiplicações entre as unidades para simplificá-las ao máximo.

Uma noção importante na análise dimensional é que algumas unidades podem ser escritas em linha e isso é comum em certos exercícios, pois a notação torna-se mais compacta. Observe o exemplo seguinte, nele mostramos a análise dimensional da grandeza aceleração:

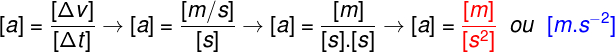
Fazendo a análise dimensional da aceleração, encontramos que a sua unidade é o metro por segundo ao quadrado (m/s²), entretanto, essa unidade pode ser escrita de forma compacta como simplesmente m.s^-2.

Veja também: Tudo sobre aceleração

Existe também a possibilidade de ser necessária a determinação de alguma grandeza física mais complexa, como no exemplo que mostraremos a seguir. Nele, faremos a determinação da unidade de medida da grandeza chamada de calor específico, muito utilizada nos cálculos de calorimetria, confira:

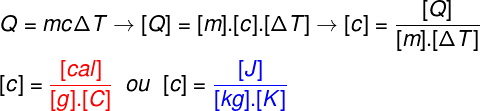
Na análise dimensional apresentada, foi necessário que rearranjássemos a equação de modo a encontrarmos qual seria a expressão para o calor específico ([c]). Feito isso, seguimos trocando as unidades de cada grandeza física até encontrarmos duas respostas diferentes: em azul, a unidade de calor específico para o SI, e, em vermelho, a unidade usual de calor específico.

É possível que haja também a necessidade de se determinar a unidade de medida de alguma grandeza fictícia. Nesse caso, elaboramos um exemplo de uma grandeza Y, que é dada pelo produto de um comprimento ([L]), por uma área ([A]) e um intervalo de tempo ([t]), divididos por uma massa ([m]).

Para determinarmos a unidade de medida dessa grandeza, de acordo com o SI, é necessário que lembremos que a unidade de comprimento é o metro (m), que a unidade de área é o metro quadrado (m²), que a unidade de tempo é o segundo (s) e que a unidade de massa é o quilograma (kg). O método utilizado para descobrirmos a unidade de Y é chamado de princípio da homogeneidade, ou seja, o lado esquerdo da equação deve ter a mesma unidade que o lado direito.

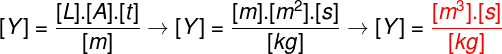
Conversão de unidades por meio da análise dimensional

Usando a análise dimensional e a correspondência entre diferentes sistemas de medida, é possível transformarmos grandezas derivadas como velocidade, aceleração, força etc. As grandezas derivadas são compostas de duas ou mais grandezas físicas fundamentais e, às vezes, é necessário transformá-las em outras unidades. O exemplo mais comum dessa aplicação da análise dimensional é a transformação da velocidade medida em metros por segundo para quilômetros por hora e vice-versa.

O segredo para fazer essa conversão de unidades de maneira correta é sempre multiplicar a unidade por 1 de maneira conveniente: alterando sua unidade de medida sem alterar o seu “valor”. Dessa forma, apesar de encontrarmos uma medida diferente para a grandeza a ser convertida, sua escala terá sido mantida. Confira um exemplo:

Na conversão apresentada, precisamos identificar que 1 km equivale a 1000 m e que 1 h equivale a 3600 s. Após isso, multiplicamos o valor da velocidade que estava medida em quilômetros por hora, por 1, isso é, 1000 m dividido por 1 km e 1 h dividida por 3600 s. Dessa forma, foi possível mudar a unidade e encontrarmos qual seria o módulo dessa velocidade na unidade de metros por segundo.

Veja também: Tudo sobre as Leis de Newton

Análise dimensional no Enem

Existem diversas questões do Enem em que é necessário fazer uso da análise dimensional para a conversão de unidades de maneira correta. No entanto, as questões do Enem não deixarão isso explícito na maioria das vezes. Será necessário perceber que as unidades estão inconsistentes, ou seja, não-homogêneas.

Confira alguns exemplos de exercícios do Enem que envolvem análise dimensional:

Questão 1) O mapa ao lado representa um bairro de determinada cidade, no qual as flechas indicam o sentido das mãos do tráfego. Sabe-se que esse bairro foi planejado e que cada quadra representada na figura é um terreno quadrado, de lado igual a 200 metros. Desconsiderando-se a largura das ruas, qual seria o tempo, em minutos, que um ônibus, em velocidade constante e igual a 40 km/h, partindo do ponto X, demoraria para chegar até o ponto Y?

a) 25 min

b) 15 min

c) 2,5 min

d) 1,5 min

e) 0,15 min

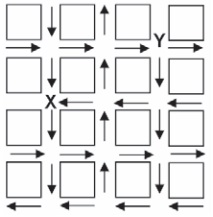
Para resolvermos esse exercício, utilizaremos a fórmula de velocidade média. De acordo com o enunciado, a velocidade do ônibus é de 40 km/h e desejamos descobrir o tempo necessário, em minutos, para que ele saia do ponto X e chegue ao ponto Y, respeitando os sentidos de cada via. Para tanto, será necessário determinar qual é a distância percorrida pelo ônibus.

Analisando o sentido das setas, verificamos que o ônibus precisa deslocar-se para o sul, movendo-se uma quadra, em seguida, precisa deslocar-se para o oeste, andando uma quadra, em seguida, desloca-se mais duas quadras para o norte e, em seguida, uma quadra para o oeste. Como cada quadra tem comprimento de 200 m, ao final do trajeto, o ônibus terá andado um total de 1000 m. Vamos fazer o cálculo:

Para resolvermos o exercício, primeiramente transformamos a velocidade do ônibus em quilômetros por minuto. Depois, descobrimos o seu deslocamento em quilômetros, utilizando a análise dimensional e a comparação entre as grandezas. Por fim, aplicamos os valores encontrados na fórmula da velocidade média.

Veja também: Tudo sobre a mecânica que cai no Enem

Questão 2) Embora o índice de Massa Corporal (IMC) seja amplamente utilizado, existem ainda inúmeras restrições teóricas ao uso e às faixas de normalidade preconizadas. O Recíproco do Índice Ponderal (RIP), de acordo com o modelo alométrico, possui uma melhor fundamentação matemática, já que a massa é uma variável de dimensões cúbicas e altura, uma variável de dimensões lineares. As fórmulas que determinam esses índices são:

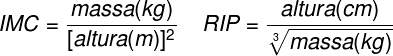
Se uma menina, com 64 kg de massa, apresenta IMC igual a 25 kg/m², então ela possui RIP igual a:

a) 0,4 cm/kg^1/3

b) 2,5 cm/kg^1/3

c) 8 cm/kg^1/3

d) 20 cm/kg^1/3

e) 40 cm/kg^1/3

Para começar a resolução desse exercício, devemos fazer a análise dimensional das duas grandezas, o IMC e o RIP:

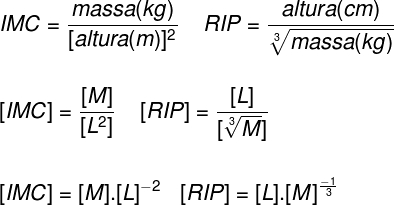
Como sabemos o IMC e a massa da menina, fica fácil encontrarmos a altura dela. Depois disso, basta aplicarmos na fórmula do RIP esses valores, transformando a altura da menina em centímetros, de modo a calculá-lo.

Veja também: Confira como estudar Física para a prova do Enem

Exercícios resolvidos

Questão 1) Determine a dimensão da grandeza física X, definida pelas dimensões mostradas abaixo, de acordo com o Sistema Internacional de Unidades:

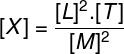
a) m^-²s¹kg^-²

b) m²s¹kg^-²

c) m²s¹kg^-3

d) m²s^-¹kg^-²

e) m²s¹kg^-1

Gabarito: Letra B

Resolução:

Para resolvermos o exercício, devemos nos lembrar de que L designa a grandeza comprimento, definida em metros, T é usado para designar a grandeza tempo, medida em segundos, e M é usado para designar a grandeza massa, medida em quilogramas. Dessa forma, basta substituirmos essas grandezas em suas respectivas dimensões:

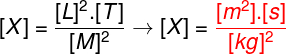
Escrevendo essa unidade em linha, teremos o seguinte resultado: m².s¹.kg^-2.

Questão 2) Determine qual deve ser a unidade da constante eletrostática k₀, de acordo com a Lei de Coulomb:

Em que Q e q são medidas em C – Coulomb, d é a distância medida em m – metros e F é a força elétrica, medida em N – Newton. Logo, para descobrirmos a unidade de k₀, devemos fazer a seguinte análise dimensional:

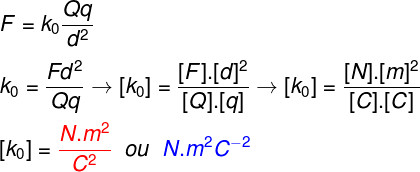
Portanto, de acordo com a análise dimensional feita, a unidade de medida da constante k0 é o N.m².C^-2.

Por Me. Rafael Helerbrock