O que são vetores?

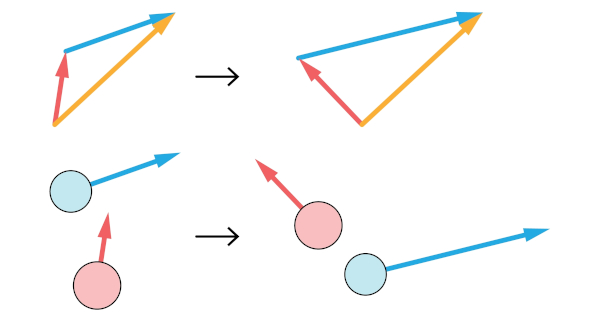
Os vetores são segmentos de reta responsáveis por caracterizar grandezas físicas vetoriais, tais como força, velocidade, aceleração e distância. Tratam dos módulos, dados pelo seu tamanho, e das suas orientações, dadas pela sua direção e sentido. Os vetores podem ser classificados em iguais, nulos, perpendiculares, oblíquos, opostos, unitários e resultantes.

Leia também: Quais são as grandezas da Física?

Tópicos deste artigo

• 1 - Resumo sobre vetores
• 2 - Videoaula sobre vetores
• 3 - Características dos vetores
  • Módulo de um vetor
  • Direção de um vetor
  • Sentido de um vetor
• 4 - Tipos de vetores
  • Vetores iguais
  • Vetores opostos
  • Vetores perpendiculares
  • Vetores oblíquos
  • Vetores nulos
  • Vetores unitários
  • Vetores resultantes
• 5 - Operações com vetores
  • Adição de vetores
  • Subtração de vetores
  • Produto de um número real por um vetor
  • Vetores perpendicualres: regra do paralelogramo e o teorema de Pitágoras
  • Vetores oblíquos: regra do paralelogramo e lei dos cossenos
  • Vetor resultante de vários vetores
• 6 - Decomposição vetorial
• 7 - Exercícios resolvidos sobre decomposição vetorial

Resumo sobre vetores

• Os vetores são caracterizados pelo seu módulo, direção e sentido.

• O vetor resultante é o vetor que resulta das operações vetoriais.

• As operações com vetores envolvem suas adições, subtrações e multiplicações por um número real.

• Os vetores perpendiculares são calculados por meio do teorema de Pitágoras.

• Os vetores oblíquos são calculados por meio da lei dos cossenos e orientados pela regra do paralelogramo.

• Os vetores podem ser decompostos na sua componente horizontal em x e na sua componente vertical em y.

Videoaula sobre vetores

Características dos vetores

Os vetores são representados por uma letra com uma seta acima — por exemplo, \(\vec{v}\), \(\vec{s}\) e \(\vec{a}\) — e caracterizados pelo seu módulo e orientação, dados pela sua direção e sentido.

• Módulo de um vetor

O módulo, comumentemente chamado de intensidade ou valor numérico, diz respeito ao tamanho da grandeza vetorial, sendo representado por \(|\vec{v} |\) ou apenas v.

• Direção de um vetor

A direção informa a posição do vetor, podendo ser horizontal, vertical e diagonal.

• Sentido de um vetor

O sentido informa a posição na qual a ponta do vetor está apontando, podendo ser direita, esquerda, para cima, para baixo, leste, norte, sul, oeste, nordeste, noroeste, sudeste, sudoeste etc.

Tipos de vetores

Os vetores podem ser tipificados como vetores iguais, vetores nulos, vetores opostos e vetores unitários.

• Vetores iguais

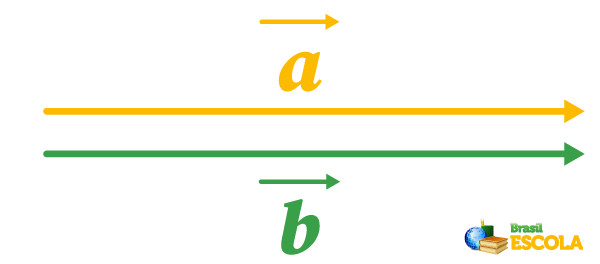
Os vetores iguais são aqueles que apresentam a mesma direção, sentido e módulo, como podemos ver na imagem abaixo:

• Vetores opostos

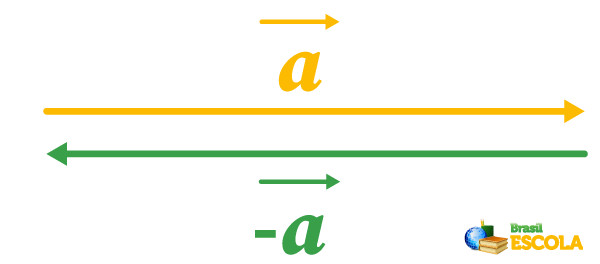
Os vetores opostos são aqueles que apresentam sentidos opostos, sendo representados por um sinal negativo na frente do símbolo do vetor.

• Vetores perpendiculares

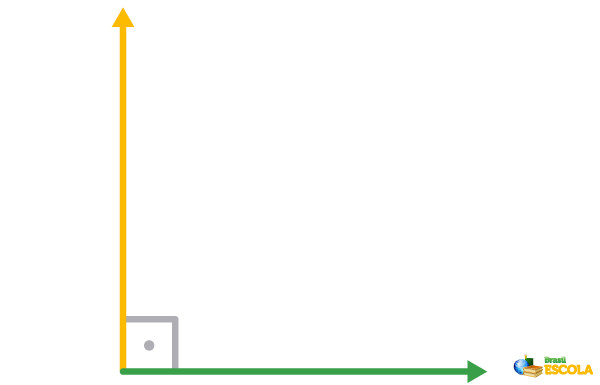
Os vetores perpendiculares são a combinação entre vetores com direções opostas que formam um ângulo de 90°.

• Vetores oblíquos

Os vetores oblíquos são a combinação entre vetores com direções opostas que formam um ângulo diferente de 0°, 90° e 180°.

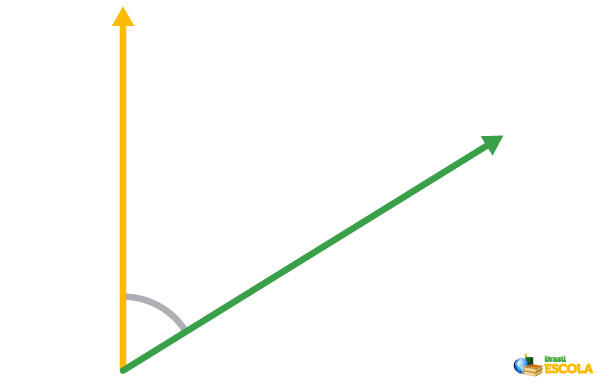
• Vetores nulos

Os vetores nulos são aqueles que apresentam módulo igual a zero e direção e sentido indeterminados. São representados geometricamente por apenas um ponto e escrito como \(\vec{0}\).

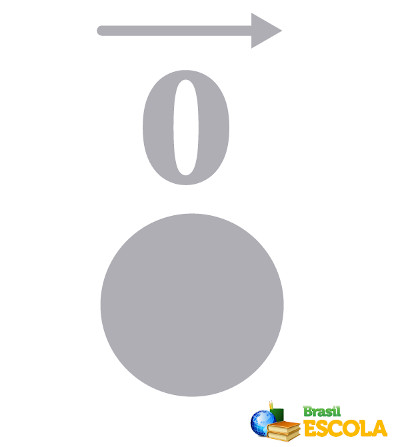
• Vetores unitários

Os vetores unitários são aqueles que apresentam módulo igual a 1.

• Vetores resultantes

O vetor resultante é aquele que resulta das operações com vetores. Para determiná-lo com exatidão, é essencial levar em consideração o módulo, direção e sentido dos vetores utilizados na operação vetorial.

Leia também: Diferenças entre grandezas escalares e vetoriais

Operações com vetores

As operações com vetores são operações algébricas realizadas por meio do módulo, direção e sentido dos vetores, sendo elas descritas abaixo:

• Adição de vetores

A adição de vetores é o somatório dos módulos (ou tamanhos) e sentidos dos vetores que obrigatoriamente estão no mesmo sentido e direção.

Exemplo: Determine o vetor resultante da adição dos vetores \(\vec{a}\) e \(\vec{b}\), com tamanho de 1 unidade e de 4 unidades, respectivamente, com suas orientações descritas na imagem abaixo:

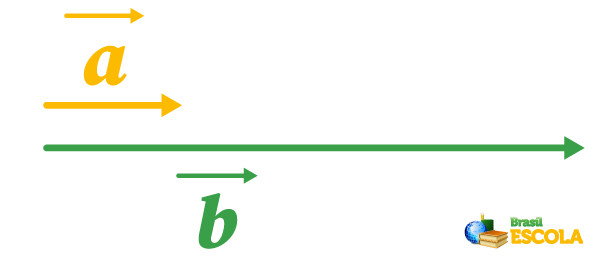
O vetor resultante da adição dos vetores \(\vec{a}\) e \(\vec{b}\) possui direção horizontal e sentido para a direita. Já seu tamanho é calculado por meio do somatório dos tamanhos dos vetores \(\vec{a}\) e \(\vec{b}\):

\(vetor\ resultante= \vec{a}+ \vec{b}\)

\(vetor\ resultante= 1+4\)

\(vetor\ resultante=5 u\)

A direção do vetor resultante é horizontal, o sentido do vetor resultante é para a direita e o tamanho do vetor resultante é de 5 unidades.

• Subtração de vetores

A subtração de vetores é a diferença dos módulos (ou tamanhos) e sentidos dos vetores. Eles precisam, obrigatoriamente, ter a mesma direção e sentido oposto.

Exemplo: Determine o vetor resultante da subtração dos vetores \(\vec{a}\) e \(\vec{b}\), com tamanhos de 2 unidades e de 3 unidades, respectivamente, com suas orientações descritas na imagem abaixo:

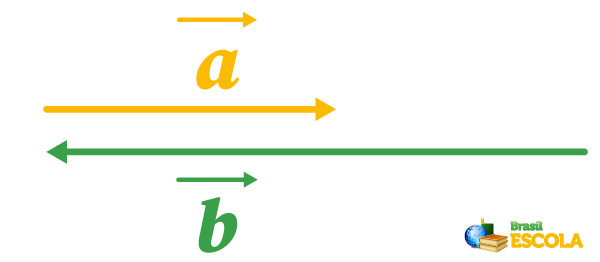
O vetor resultante da subtração dos vetores \(\vec{a}\) e \(\vec{b}\) possui direção horizontal e sentido para a esquerda, sendo no mesmo sentido que o vetor com maior tamanho. Já seu tamanho é calculado por meio da subtração dos tamanhos dos vetores \(\vec{a}\) e \(\vec{b}\):

\(vetor\ resultante= \vec{a}- \vec{b}\)

\(vetor\ resultante=2-3\)

\(vetor\ resultante=-1\ u\)

A direção do vetor resultante é horizontal, o sentido do vetor resultante é para a esquerda, e o tamanho do vetor resultante é de 1 unidade. O sinal negativo significa que ele está contrário ao sentido do vetor \(\vec{a}\).

• Produto de um número real por um vetor

O produto de um número real por um vetor gera um vetor novo, com mesma direção e sentido para o caso de o número real ser positivo e mesma direção e sentido oposto para o caso de o número real ser negativo. Seu módulo é o resultado do produto entre o número real n e o vetor \(\vec{v}\), conforme descrito na fórmula abaixo:

\(v_{novo}=n\cdot \vec{v}\)

Exemplo: Determine o vetor resultante da multiplicação do número real 10 pelo vetor \(\vec{a}\) com módulo de 15 unidades e orientação sudoeste.

Nesse caso, a direção e o sentido do vetor permanecem os mesmos — diagonal e sudoeste, respectivamente. Já o módulo é calculado por meio da fórmula abaixo:

\(v_{novo}=n\cdot \vec{v}\)

\(v_{novo}=10\cdot 15\)

\(v_{novo}=150\ u\)

A direção do vetor resultante é diagonal, o sentido do vetor resultante é sudoeste, e o módulo do vetor novo é de 150 unidades.

• Vetores perpendicualres: regra do paralelogramo e o teorema de Pitágoras

Nos vetores perpendiculares, o módulo é calculado por meio do teorema de Pitágoras, com a sua equação:

\(hipotenusa^2=cateto_1^2+cateto_2^2\)

Exemplo: Determine o vetor resultante da combinação dos vetores \(\vec{a}\) e \(\vec{b}\), com tamanhos de 3 unidades e de 5 unidades, respectivamente, e com suas orientações descritas na imagem abaixo:

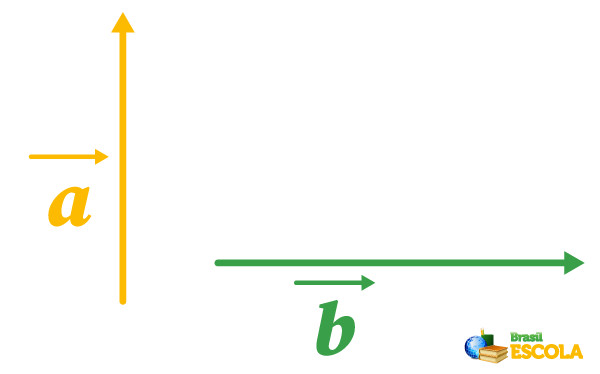
Para encontrarmos sua direção e sentido, usaremos a regra do paralelogramo, que consiste primeiramente em unir os dois vetores pela sua origem, conforme desenhado abaixo:

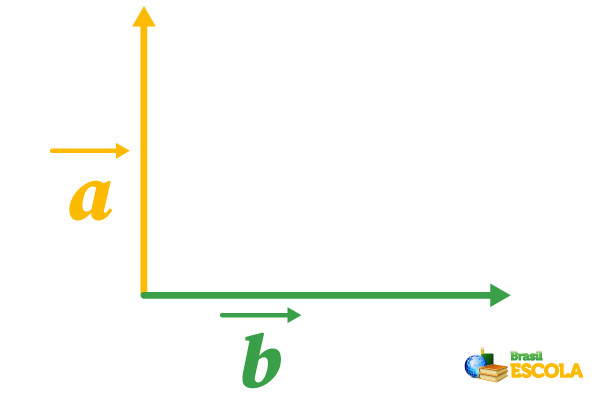
Depois, traçaremos pontilhados do mesmo tamanho dos vetores, conforme desenhado abaixo:

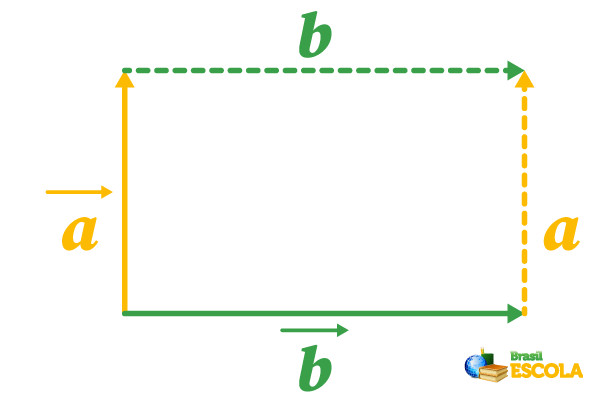
Em seguida, traçaremos uma linha diagonal, unindo a ponta da origem dos vetores até o ponto em que suas setas se encontram. Essa linha corresponde ao vetor resultante \(\vec{r}\) entre esses dois vetores, como desenhado abaixo:

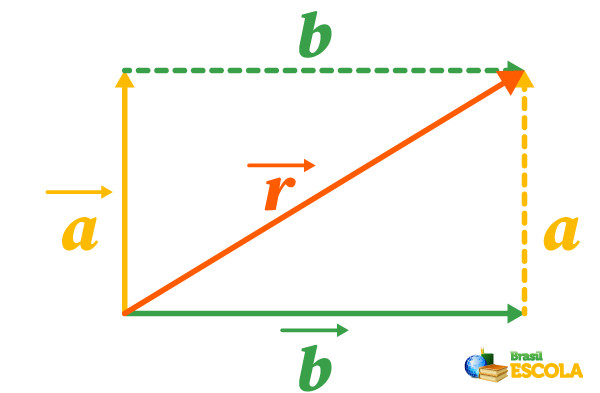
Já o módulo do vetor resultante é calculado por meio do teorema de Pitágoras, dado pela fórmula:

\(hipotenusa^2=cateto_1^2+cateto_2^2\)

A hipotenusa corresponde ao módulo do vetor resultante \(\vec{r}\), e os catetos são os módulos dos vetores envolvidos:

\(r^2=a^2+b^2\)

\(r^2=3^2+5^2\)

\(r^2=9+25\)

\(r^2=34\)

\(r=\sqrt{34}\)

A direção do vetor resultante é diagonal, o sentido do vetor resultante é nordeste, e o tamanho do vetor resultante é de \(\sqrt{34}\) unidades.

• Vetores oblíquos: regra do paralelogramo e lei dos cossenos

Nos vetores oblíquos, a direção e sentido são dados por meio da regra do paralelogramo e o módulo é calculado por meio da lei dos cossenos, com a sua fórmula:

\(hipotenusa^2=cateto_1^2+cateto_2^2-2\cdot cateto_1\cdot cateto_2\cdot cos \theta \)

Exemplo: Determine o vetor resultante da combinação dos vetores \(\vec{a}\) e \(\vec{b}\), com tamanhos de 4 unidades e de 7 unidades, respectivamente, sabendo que o ângulo formado entre eles é 60° e suas orientações estão descritas na imagem abaixo:

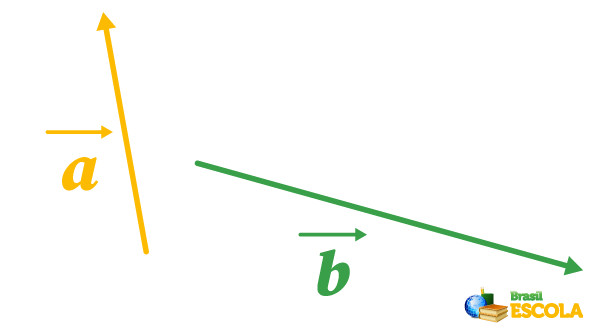
Para encontrarmos sua direção e sentido, usaremos também a regra do paralelogramo, como explicada no exemplo anterior, resultando na imagem abaixo:

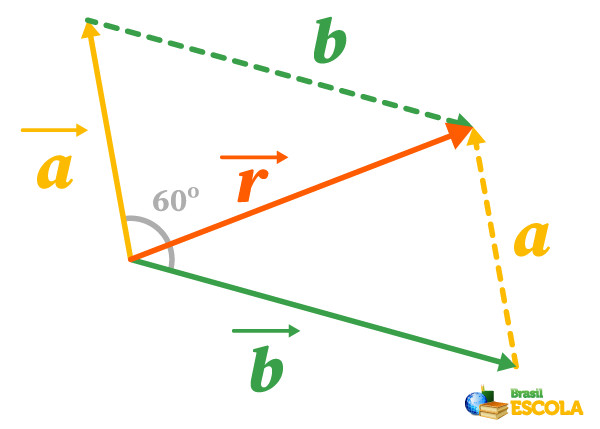
Já o módulo do vetor resultante é calculado por meio da lei dos cossenos, dada pela fórmula:

\(hipotenusa^2=cateto_1^2+cateto_2^2-2cateto_1\cdot cateto_2\cdot cos \theta \)

A hipotenusa corresponde ao módulo do vetor resultante \(\vec{r}\), e os catetos são os módulos dos vetores envolvidos:

\(r^2=a^2+b^2-2\cdot a\cdot b\cdot cos \theta \)

\(r^2=4^2+7^2-2\cdot 4\cdot 7\cdot cos\ 60°\)

\(r^2=16+49-56\cdot 0,5\)

\(r^2=16+49-28\)

\(r^2=37\)

\(r=\sqrt{37}\)

A direção do vetor resultante é diagonal, o sentido do vetor resultante é para a direita, e o tamanho do vetor resultante é \(\sqrt{37}\) unidades.

• Vetor resultante de vários vetores

O vetor resultante de vários vetores é dado por meio da união das origens dos vetores e calculado pelo vetor resultante de dois em dois vetores, utilizando as operações de adição ou subtração, o teorema de Pitágoras ou a lei dos cossenos.

Exemplo: Determine o vetor resultante da combinação dos vetores \(\vec{a}\), \(\vec{b}\) e \(\vec{c}\), com tamanhos de 3, 4 e 5 unidades, respectivamente, sabendo que o ângulo formado entre \(\vec{a}\) e \(\vec{b}\) é de 60°, o ângulo formado entre o vetor resultante entre os vetores \(\vec{a}\) e \(\vec{b}\) com o vetor \(\vec{c}\) é de 30° e suas orientações estão descritas na imagem abaixo:

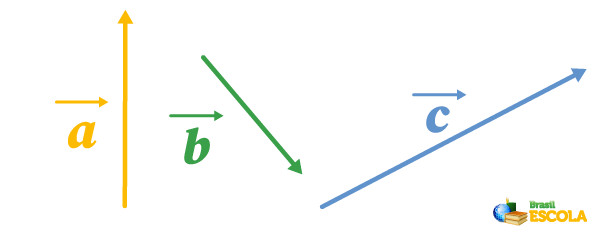
Primeiramente, vamos unir as origens dos vetores, como na imagem abaixo:

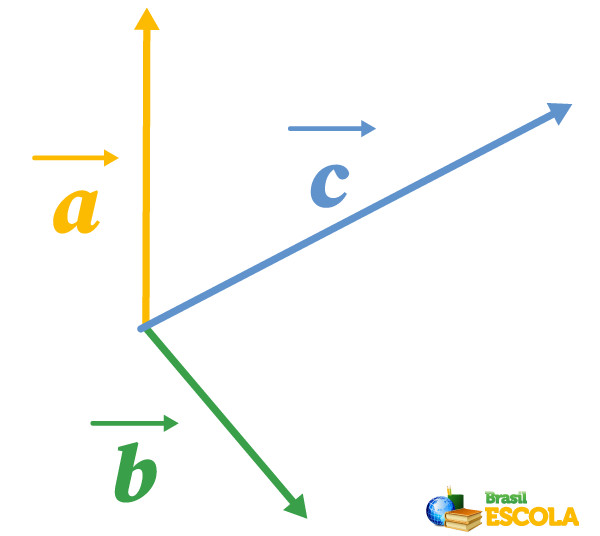
Depois, encontraremos o sentido e direção do vetor resultante entre os vetores \(\vec{a}\) e \(\vec{b}\), chamado-o de vetor \(\vec{v}\), por meio da regra do paralelogramo, como na imagem abaixo:

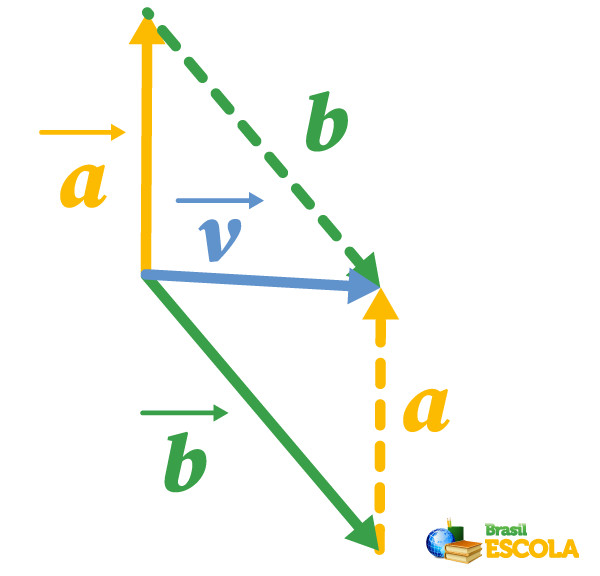
Já o módulo do vetor resultante \(\vec{v}\) é calculado por meio da lei dos cossenos, dada pela fórmula:

\(hipotenusa^2=cateto_1^2+cateto_2^2-2\cdot cateto_1\cdot cateto_2\cdot cos \theta \)

A hipotenusa corresponde ao módulo do vetor resultante \(\vec{v}\), e os catetos são os módulos dos vetores envolvidos:

\(v^2=a^2+b^2-2\cdot a\cdot b\cdot cos\ 60°\)

\(v^2=3^2+4^2-2\cdot 3\cdot 4\cdot 0,5\)

\(v^2=9+16-24\cdot 0,5\)

\(v^2=9+16-12\)

\(v^2=13\)

\(v=\sqrt{13}\ u\)

Em seguida, encontraremos o sentido e direção do vetor resultante entre os vetores \(\vec{v}\) e \(\vec{c}\), chamado-o de vetor \(\vec{r}\), por meio da regra do paralelogramo, como na imagem abaixo:

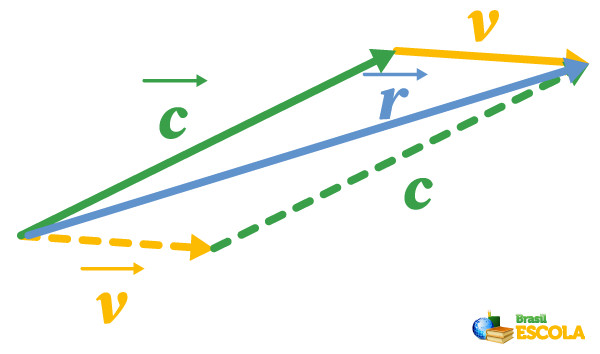
Já o módulo do vetor resultante \(\vec{r}\) é calculado por meio da lei dos cossenos, dada pela fórmula:

\(hipotenusa^2=cateto_1^2+cateto_2^2-2\cdot cateto_1\cdot cateto_2\cdot cos \theta \)

A hipotenusa corresponde ao módulo do vetor resultante \(\vec{r}\), e os catetos são os módulos dos vetores envolvidos:

\(r^2=v^2+c^2-2\cdot v\cdot c\cdot cos\ 30°\)

\(r^2=13+25-5\cdot \sqrt{39}\)

\(r^2\cong 13+25-5\cdot 6,24\)

\(r^2\cong 38-31,22\)

\(r^2\cong 6,77\)

\(r\cong 2,6\ u\)

A direção do vetor resultante é diagonal, o sentido do vetor resultante é leste-nordeste, e o tamanho do vetor resultante é de aproximadamente 2,6 unidades.

Para saber mais sobre as operações com vetores e conferir mais exemplos, clique aqui.

Decomposição vetorial

A decomposição vetorial é a fragmentação de um vetor em sua componente horizontal x e componente vertical y. O cálculo pode ser feito por meio das fórmulas abaixo:

\(a_x=a\cdot cos \theta \)

- \(a_x\) é o módulo da componente horizontal do vetor \(\vec{a}\).

- a é o módulo do vetor \(\vec{a}\).

- \(cos \theta \)  é o cosseno do ângulo formado entre o vetor a  e a sua componente horizontal \(\vec{a_x}\).

\(a_y=a\cdot sin \theta \)

- \(a_y \) é o módulo da componente vertical do vetor \(\vec{a}\).

- a é o módulo do vetor \(\vec{a}\).

- \(sin \theta \) é o seno do ângulo formado entre o vetor \(\vec{a}\) e a sua componente horizontal \(\vec{a_x}\).

Exemplo: Encontre e calcule a componente horizontal e a componente vertical do vetor \(\vec{a}\) com orientação nordeste e módulo de 5 unidades, sabendo que o ângulo formado entre ele e a sua componente horizontal é de 30°.

Primeiramente, desenharemos o vetor \(\vec{a}\):

Então, vamos decompô-lo em suas componentes x e y da seguinte forma:

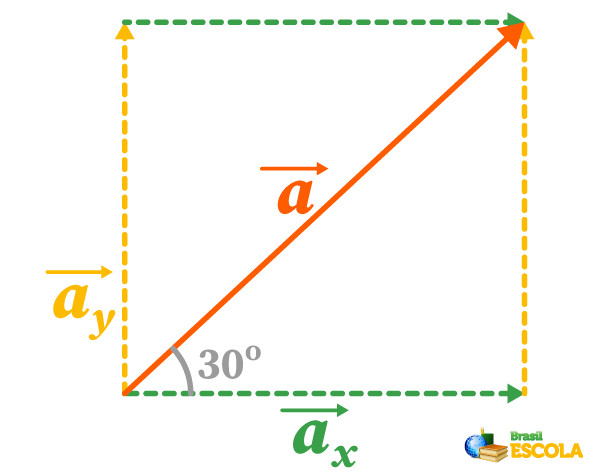
Depois, calcularemos a componente horizontal, por meio da sua fórmula:

\(a_x=a\cdot cos \theta \)

\(a_x=5\cdot cos\ 30°\)

\(a_x=5\cdot \frac{\sqrt{2}}2\)

\(a_x=2,5\sqrt{2}\ u\)

Por fim, calcularemos a componente vertical, por meio da sua fórmula:

\(a_y=a\cdot sin \theta \)

Exercícios resolvidos sobre decomposição vetorial

Questão 1

(UEPG-PR) Quando dizemos que a velocidade de uma bola é de 20 m/s, horizontal e para a direita, estamos definindo a velocidade como uma grandeza:

a) escalar

b) algébrica

c) linear

d) vetorial

e) n.d.a.

Resolução:

Alternativa D. Toda grandeza que necessita de orientação, além da intensidade, é chamada de grandeza vetorial.

Questão 2

(Fesp) Em um corpo estão aplicadas apenas duas forças, de intensidades 12 N e 8,0  N. Uma possível intensidade da resultante será:

a) 22 N

b) 3,0 N

c) 10 N

d) zero

e) 21 N

Resolução:

Alternativa C. Como não nos foi informada a orientação dos vetores, a intensidade do vetor resultante pode ser dada pelas operações de dois vetores. Então, primeiramente calcularemos utilizando a adição de vetores:

\(\vec{v}+\vec{u}=12+8=20\ N\)

Em seguida, calcularemos a subtração de vetores:

\(\vec{v}-\vec{u}=12-8=4\)

Depois, consideraremos os vetores como perpendiculares e os calcularemos com o teorema de Pitágoras:

\(hipotenusa^2=cateto_1^2+cateto_2^2\)

\(vetor\ resultante^2=12^2+8^2\)

\(vetor\ resultante^2=144+64\)

\(vetor\ resultante^2=208\)

\(vetor\ resultante=\sqrt{208}\)

\(vetor\ resultante\cong 14,42\)

Por fim, consideraremos os vetores como oblíquos e os calcularemos por meio da regra do paralelogramo:

\(hipotenusa^2=cateto_1^2+cateto_2^2-2\cdot cateto_1\cdot cateto_2\cdot cos \theta \)

\(vetor\ resultante^2=12^2+8^2-2\cdot 12\cdot 8\cdot cos \theta \)

Não temos o ângulo, mas sabemos que o menor valor e o maior valor do cosseno de um ângulo são -1 e 1, respectivamente, então realizaremos um cálculo para cada um desses valores:

Cosseno do ângulo 1:

\(vetor\ resultante^2=144+64-2\cdot 12\cdot 8\cdot 1\)

\(vetor\ resultante^2=144+64-192\)

\(vetor\ resultante^2=16\)

\(vetor\ resultante=\sqrt{16}\)

\(vetor\ resultante=4\)

Cosseno do ângulo -1:

\(vetor\ resultante^2=144+64-2\cdot 12\cdot 8\cdot (-1)\)

\(vetor\ resultante^2=400\)

\(vetor\ resultante=\sqrt{400}\)

\(vetor\ resultante=20\)

Os valores possíveis de intensidade resultante são 4, 14, 42 e 20, então uma possível intensidade da resultante está entre 4 e 20, sendo 10.

Por Pâmella Raphaella Melo
Professora de Física