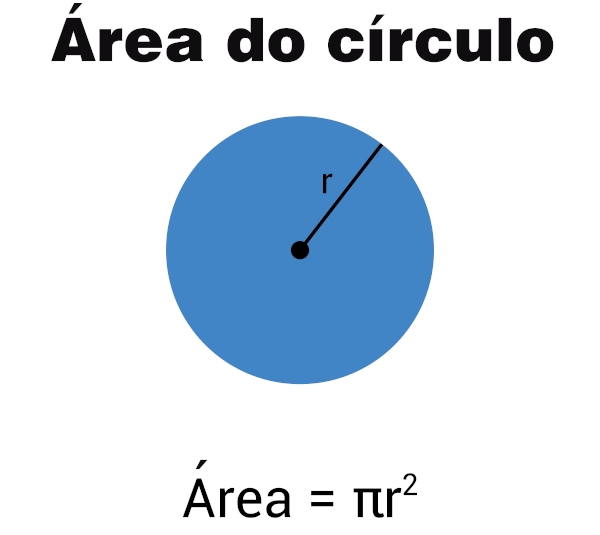
A área do círculo é a medida da superfície dessa figura geométrica. Para calcular a área de um círculo, é suficiente conhecer a medida de seu raio, que é a distância entre o centro e a borda. A fórmula para calcular a área do círculo é:
\(A=\pi r^2\)
Leia também: Área do setor circular — uma fatia da circunferência
Tópicos deste artigo
- 1 - Resumo sobre área do círculo
- 2 - O que é círculo?
- 3 - Fórmula da área do círculo
- 4 - Como calcular a área do círculo?
- 5 - Círculo X circunferência
- 6 - Perímetro do círculo
- 7 - Exercícios sobre área do círculo
Resumo sobre área do círculo
- A área do círculo é a medida de sua superfície.
- Dado um círculo de raio r, sua área A é determinada pela expressão:
\(A=\pi r^2\)
- O círculo é a região interna da circunferência.
- O perímetro do círculo é a medida do seu contorno, que é o comprimento da circunferência de mesmo raio.
- A fórmula do perímetro C do círculo é:
\(C=2\pi r\)
O que é círculo?
Considere um ponto P e uma medida r. O círculo de centro P e raio r são o conjunto de pontos que estão a uma distância igual ou menor que r do ponto P. Na imagem adiante, a região em roxo é o círculo de centro P e raio r.
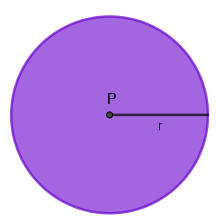
Formalmente, dizemos que os pontos A que pertencem ao círculo satisfazem a seguinte condição:
\(d\left(A,P\right)\le r\)
Lemos: A distância entre A e P é menor ou igual a r.
Fórmula da área do círculo
A fórmula da área do círculo está diretamente relacionada ao seu raio. Em um círculo de raio r, sua área A é obtida pela fórmula:
\(A_{círculo}=πr^2\)
Em que π é um número irracional aproximadamente igual a 3,1415.
Veja também: Como encontrar os ângulos de uma circunferência?
Como calcular a área do círculo?
Vejamos alguns exemplos de como calcular a área do círculo utilizando sua fórmula. Observe, em cada caso, a relação entre a unidade de medida do raio e unidade de medida da área.
- Exemplo 1: Determine a área de um círculo de 8 cm de raio. (Utilize π=3,14)
Como r = 8 cm, temos que:
\(A=3,14\cdot8^2\)
\(A=\ 3,14\cdot64\)
\(A=200,96 cm²\)
- Exemplo 2: Qual a área de um círculo com 12,5 m de raio? (Considere π=3)
Como r = 12,5 m, temos que:
\(A=3\cdot\left(12,5\right)^2\)
\(A=3\cdot156,25\)
\(A=468,75 m²\)
Círculo X circunferência
Círculo e circunferência não são a mesma figura. A circunferência é a borda, o contorno do círculo. A imagem adiante é uma circunferência de raio r.
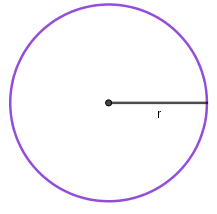
-> Videoaula sobre círculo e circunferência
Perímetro do círculo
O perímetro do círculo é a medida de seu contorno. Assim, o perímetro de um círculo de raio r é o comprimento da circunferência de raio r, cuja fórmula é:
\(C=2\pi r\)
- Exemplo: Uma pessoa caminha ao longo da borda de uma piscina circular, completando exatamente uma volta. Qual a distância que essa pessoa percorreu se o raio da piscina é igual a 30 metros? (Utilize π = 3,14)
\(C=2\cdot3,14\cdot30\)
\(C=188,4 metros\)
Exercícios sobre área do círculo
Questão 1
(Uerj) Um valor aproximado da área do círculo pode ser obtido elevando-se ao quadrado 8/9 do seu diâmetro. Fazer esse cálculo corresponde a substituir, na fórmula da área do círculo, o valor de π por um número racional.
Esse número é igual a:
a) \( \frac{128}{9}\)
b) \( \frac{256}{9}\)
c) \( \frac{128}{81}\)
d) \( \frac{256}{81}\)
Resolução
Letra D
O diâmetro de um círculo é o dobro do raio. Assim, de acordo com o enunciado, temos a seguinte aproximação para a área do círculo:
\(A=\left(\frac{8}{9}d\right)^2\)
\(A=\left(\frac{8}{9}2r\right)^2\)
\(A=\left(\frac{16}{9}r\right)^2\)
\(A=\frac{256}{81}r^2\)
Comparando essa expressão com a fórmula da área do círculo, \(A=\pi r^2\), temos que o valor de π deve ser substituído por \(\frac{256}{81}\).
Questão 2
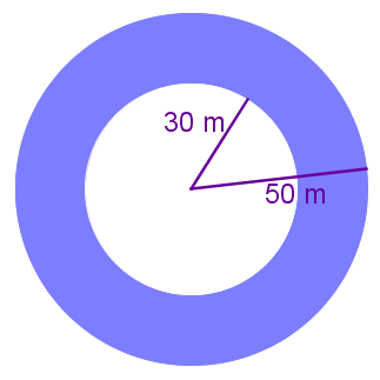
(Enem) No projeto de arborização de uma praça está prevista a construção de um canteiro circular. Esse canteiro será constituído de uma área central e de uma faixa circular ao seu redor, conforme ilustra a figura.
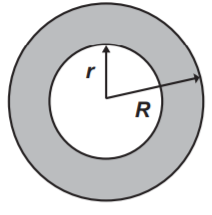
Deseja-se que a área central seja igual à área da faixa circular sombreada. A relação entre os raios do canteiro (R) e da área central (r) deverá ser:
a) \( R=2r\)
b) \( R=r\sqrt2\)
c) \( R=\frac{r^2+2r}{2}\)
d) \( R=r^2+2r\)
e) \( R=\frac{3}{2}r\)
Resolução
Letra B
Seja Aca a área do canteiro e Ace a área central, note que a área sombreada é Aca-Ace. Portanto, se a área central deve ser igual à área da faixa circular sombreada, temos que:
\(A_{ce}=A_{ca}-A_{ce}\)
\({2A}_{ce}=A_{ca}\)
Logo:
\(2\pi r^2=\pi R^2\)
\(2r^2=R^2\)
\(R=\sqrt{2r^2}\)
\(R=r\sqrt2\)
Fontes
LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.