Área da coroa circular

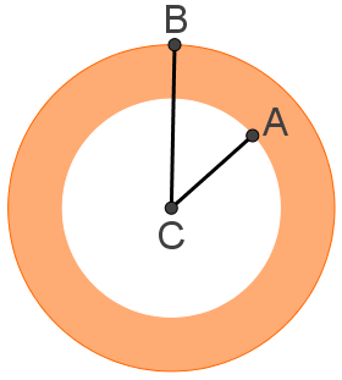
Considere uma circunferência inscrita em outra circunferência, ou seja, duas circunferências concêntricas (mesmo centro), a região plana delimitada por elas é chamada de coroa circular.

Veja ilustrações abaixo:



Assim, teremos dois raios: um da circunferência maior e outro da menor.



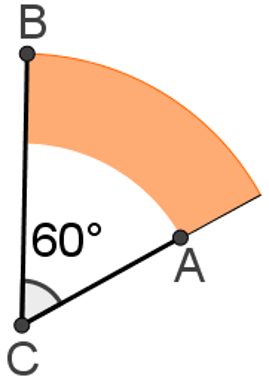
Pela figura podemos dizer que a área da coroa circular será igual à diferença da área dos dois círculos que formam a coroa:

A_coroa = A_{círculo maior} – A_{círculo menor}

A_coroa = (π . R2) - (π . r2)

A_coroa = π . (R2 - r2)

Exemplo: Determine a área da superfície colorida:



AC = AO/2
AO = 10

Como a região colorida é 1/4 da coroa circular, teremos que dividir por 4 a área total da coroa:

A_colorida = π (R2 - r2)
                       4

A_colorida = π (152 - 102)
                          4

A_colorida = π (225 – 100)
                          4

A_colorida = π 125
                     4

A_colorida = 125π cm²
                       4

Exemplo: A região colorida na figura abaixo tem 32 π/25 m² de área. Se o raio do arco mede 4m, quanto mede o raio do menor?



360° : 45° = 8, isso significa que a parte pintada corresponde a 1/8 da coroa circular, assim podemos dizer que a coroa terá área igual a:

A_coroa = 32 π/25 . 8 = 256 π / 25

Para descobrir o valor do raio menor basta aplicar a fórmula e fazer as devidas substituições:

A_coroa = π . (R2 - r2)

256 π / 25 = π . (42 - r2)

256 π / 25 = π . (16 – r2)

10,24 = 16 – r2

10,24 – 16 = – r2 (-1)

-10,24 + 16 = r2

5,76 = r2

2,4 = r

Por Danielle de Miranda
Graduada em Matemática