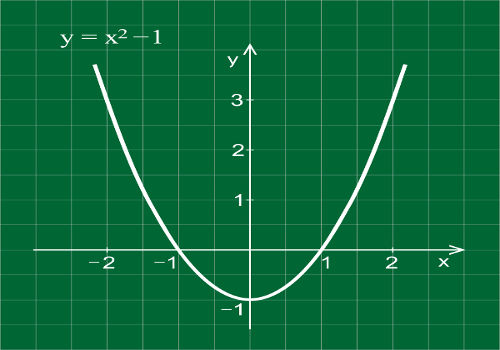
Toda expressão na forma y = ax² + bx + c ou f(x) = ax² + bx + c, com a, b e c números reais, sendo a ≠ 0, é denominada função do 2º grau. A representação gráfica de uma função do 2º grau é dada através de uma parábola, que pode ter a concavidade voltada para cima ou para baixo. Veja:
Não pare agora... Tem mais depois da publicidade ;)
.jpg)
Para determinar o ponto máximo e o ponto mínimo de uma função do 2º grau, basta calcular o vértice da parábola utilizando as seguintes expressões matemáticas:
.jpg)
O ponto máximo e o ponto mínimo podem ser atribuídos a várias situações presentes em outras ciências, como Física, Biologia, Administração, Contabilidade entre outras.
Física: movimento uniformemente variado, lançamento de projéteis.
Biologia: na análise do processo de fotossíntese.
Administração: estabelecendo pontos de nivelamento, lucros e prejuízos.
Exemplos
1 – Na função y = x² - 2x +1, temos que a = 1, b = -2 e c = 1. Podemos verificar que a > 0, então a parábola possui concavidade voltada para cima, possuindo ponto mínimo. Vamos calcular as coordenadas do vértice da parábola.
.jpg)
.jpg)
As coordenadas do vértice são (1, 0).
2 – Dada a função y = -x² -x + 3, temos que a = -1, b = -1 e c = 3. Temos a < 0, então a parábola possui concavidade voltada para baixo tendo um ponto máximo. Os vértices da parábola podem ser calculados da seguinte maneira:
.jpg)
.jpg)
As coordenadas do vértice são (-0,5; 3,25).
Concluímos que o vértice da parábola deve ser considerado um ponto notável, em razão da sua importância na construção do gráfico de uma função do 2º grau e sua relação com os pontos de valor máximo e mínimo.
Por Marcos Noé
Graduado em Matemática
