O que é concavidade de uma parábola?

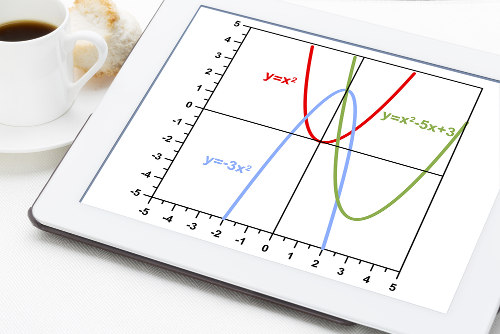
Uma parábola é a representação geométrica de uma função do segundo grau, que, por sua vez, é qualquer função que possa ser escrita na forma f(x) = ax² + bx + c. Nessa função, as letras a, b e c representam números reais constantes, chamados coeficientes. Já a letra x é chamada de variável, pois pode assumir qualquer valor dentro do domínio dessa função. O coeficiente “a” dessas funções determina a concavidade da parábola que as representa.

Concavidade da parábola

Se a função do segundo grau puder ser escrita na forma f(x) = ax² + bx + c, então ela poderá ser representada por uma parábola que, obrigatoriamente, atenderá a uma das duas condições a seguir:

Se a > 0, a concavidade da parábola é voltada para cima.

Se a < 0, a concavidade da parábola é voltada para baixo.

Portanto, coeficiente “a” de uma função do segundo grau determina para onde a concavidade dessa figura estará voltada.

O que é concavidade?

A concavidade de uma parábola é uma reentrância nessa figura e é indicada, como vimos, pelo valor do coeficiente “a”. Para compreender melhor essa questão e o que é concavidade, observe os dois casos a seguir, as discussões que os envolvem e as imagens ligadas a eles:

Caso 1: Concavidade voltada para baixo

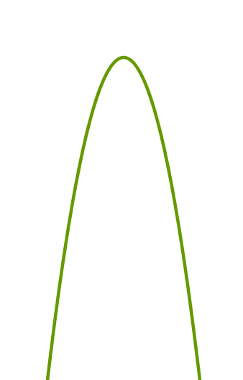
Quando a concavidade de uma parábola é voltada para baixo, essa figura possui um ponto, chamado vértice, que possui a maior coordenada y possível. No gráfico, não existe ponto que pertença a uma parábola com concavidade voltada para baixo acima do vértice. Por outro lado, dado um ponto P qualquer pertencente a essa parábola, sempre existirá outro ponto T com coordenada y menor que a coordenada y do ponto P.

A imagem a seguir mostra uma parábola com a concavidade voltada para baixo. Essas parábolas representam funções cujo coeficiente a é menor que zero.

Caso 2: Concavidade voltada para cima

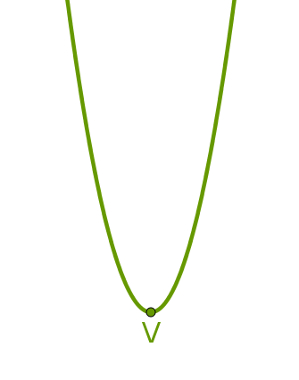
Quando a parábola possui concavidade voltada para cima, é possível encontrar nela um ponto, chamado vértice, que, entre todos os pontos da parábola, é o mais baixo. Em outras palavras, qualquer outro ponto dessa parábola terá, como coordenada y, um número maior que a coordenada y do vértice. Assim, y do vértice é a menor coordenada y possível para esse tipo de parábola.

A imagem a seguir mostra uma parábola com a concavidade voltada para cima e seu vértice. Essa parábola representa uma função do segundo grau cujo coeficiente a é maior que zero.

Por Luiz Moreira
Graduado em Matemática