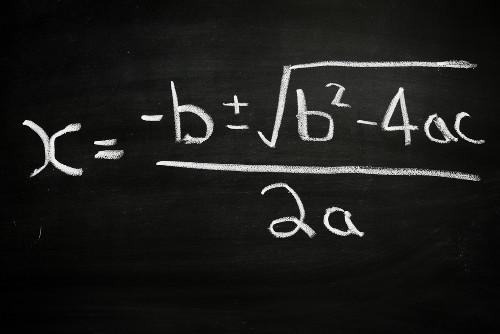O que é discriminante?

Um dos métodos usados para encontrar os resultados de uma equação do segundo grau é a fórmula de Bháskara. O uso dessa fórmula costuma ser dividido em duas etapas: a primeira consiste em encontrar o valor do discriminante da equação e a segunda em encontrar os seus resultados.

Tópicos deste artigo

• 1 - Mas, o que é "Discriminante"?

Mas, o que é "Discriminante"?

Discriminante é a parte da fórmula de Bháskara que está sob a raiz quadrada.

O cálculo do discriminante é feito substituindo os valores dos coeficientes da equação na seguinte fórmula:

Δ = b² – 4ac

A partir desse valor, basta substituí-lo, junto aos coeficientes da equação, na fórmula:

x = – b ± √Δ
       2a

A separação desse método em duas etapas é apenas didática. A fórmula de Bháskara também pode ser escrita:

x = – b ± √[b² – 4ac]
      2a

Existem outros usos para o discriminante de uma equação do segundo grau. A seguir, falaremos sobre eles.

Quantidade de soluções de uma equação do segundo grau

Muitas vezes, pode ser necessário saber se uma equação do segundo grau possui resultados reais e sua quantidade em vez de saber quais são esses resultados. Por meio do discriminante da equação do segundo grau, é possível saber essas informações.

As equações do segundo grau podem ter até dois resultados reais e distintos. Na fórmula anterior, note que antes da raiz quadrada existe um sinal “±”. Esse sinal apenas garante que um cálculo deverá ser feito tomando o valor positivo do resultado da raiz e outro cálculo deve ser feito tomando o valor negativo do resultado da raiz. Portanto, até dois resultados podem ser encontrados.

Perceba que, se o discriminante for negativo, não será possível calcular a sua raiz e, por isso, a equação não terá soluções reais.

Se o discriminante é igual a zero, a fórmula de Bháskara resume-se a:

x = – b ± √Δ
     2a

x = – b ± √0
      2a

x = – b
       2a

Como o sinal “±” está relacionado à raiz, uma equação do segundo grau com discriminante igual a zero terá apenas um resultado real.

Já as equações com discriminante maior que zero terão dois resultados reais e distintos.

Assim, podemos dizer:

Se Δ < 0, a equação não possui resultados reais.

Se Δ = 0, a equação possui um resultado real.

Se Δ > 0, a equação possui dois resultados reais.

Estudo dos sinais de uma função do segundo grau

A solução de alguns problemas envolvendo funções do segundo grau pode ser o intervalo de valores do domínio que faz com que os valores do contradomínio sejam maiores do que zero, por exemplo.

É possível usar o discriminante da equação do segundo grau para determinar se existe um intervalo no qual a função é positiva ou não. Para isso, tenha em mente que as raízes de uma função do segundo grau são os pontos de encontro dela com o eixo x.

Se Δ < 0, a função não possui raízes.

Se Δ = 0, a função possui uma raiz.

Se Δ > 0, a função possui duas raízes.

Além disso, as funções do segundo grau são parábolas. Assim, teremos as seguintes possibilidades:

Se a função do segundo grau possui Δ > 0, terá duas raízes reais e distintas. Uma parte da parábola que a representa estará acima do eixo x e a outra abaixo.

Se o coeficiente a é positivo, essa função tem ponto de mínimo abaixo do eixo x, e a função é negativa entre suas raízes. Caso contrário, tem ponto de máximo acima do eixo x, e a função será positiva entre suas raízes.

Se a função do segundo grau possui Δ = 0, terá uma raiz real. Então, a parábola tocará o eixo x em apenas um ponto. Se a for positivo, toda a função será positiva, exceto sua raiz (porque é neutra). Se a for negativo, toda a função será negativa, exceto sua raiz.

Se a função do segundo grau possui Δ < 0, então ela não possui raízes. Assim, se a é positivo, toda a função será positiva. Se a é negativo, toda a função será negativa.

Por Luiz Paulo Moreira
Graduado em Matemática