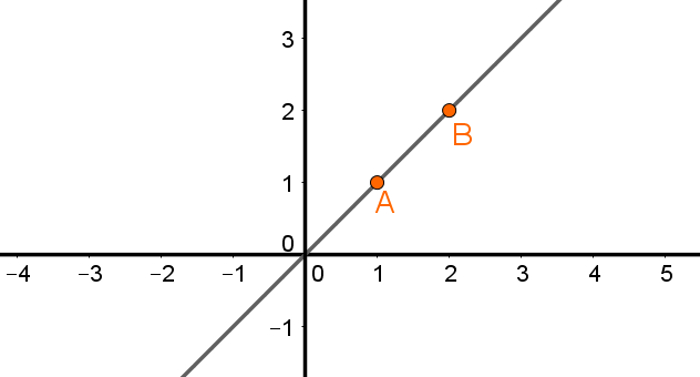
Uma função do primeiro grau é aquela cuja lei de formação pode ser escrita na seguinte forma:
y = ax + b
Na qual, a e b pertencem ao conjunto dos números reais, e a é diferente de zero. Esse tipo de função também é chamada de função afim.
É importante relembrar os principais conceitos a respeito das funções em geral para compreender bem as funções do primeiro grau.
Tópicos deste artigo
- 1 - O que é uma função?
- 2 - Mapa Mental: Gráfico de função do 1º Grau
- 3 - Exemplos de função do primeiro grau
- 4 - Exemplos de funções que não são do primeiro grau
- 5 - Gráfico da função do primeiro grau
O que é uma função?
Uma função é uma regra matemática que relaciona cada elemento x, de um conjunto A, a um único elemento y, de um conjunto B. Os conjuntos A e B são conhecidos, respectivamente, como domínio e contradomínio. Já x e y são conhecidos, respectivamente, como variável independente e variável dependente, pois o valor de y sempre dependerá do valor de x.
Assim, as funções do primeiro grau são regras que relacionam cada elemento de um conjunto a um único elemento de outro cuja variável independente é uma potência de expoente 1. O grau de uma função sempre é dado pelo maior expoente da variável independente e, no caso das funções do primeiro grau, o maior expoente é 1.
Mapa Mental: Gráfico de função do 1º Grau
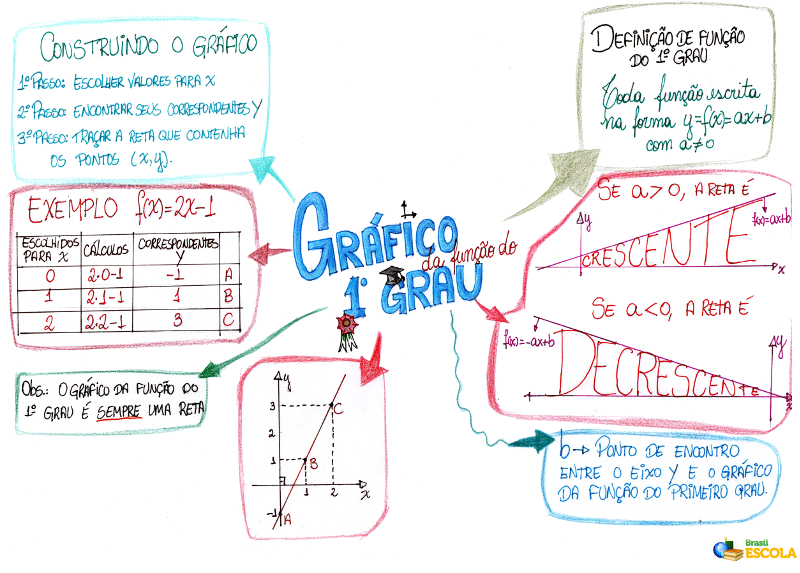
* Baixe o mapa mental sobre gráfico de função do primeiro grau!
Exemplos de função do primeiro grau
Os exemplos a seguir são de funções do primeiro grau. Isso significa que elas podem ser escritas na forma y = ax + b, ou já estão nessa forma.
a) y = 2x + 9. Essa é uma função afim, ou do primeiro grau, em que a = 2 e b = 9.
b) y = – x – 7. Embora o sinal de – 7 não seja positivo, essa também é uma função do primeiro grau, com a = – 1 e b = – 7. Para que não haja dúvidas, basta escrevê-la: y = (–1)x + (–7).
c) f(x) = 0,2x. Essa é uma função afim, ou do primeiro grau, na qual a = 0,2 e b = 0. Observe que f(x) é outra notação para y, mas ambos representam a mesma coisa.
A partir dos exemplos acima, lembre-se sempre: as funções do primeiro grau são aquelas em que a variável independente possui expoente máximo igual a 1.
Exemplos de funções que não são do primeiro grau
Para que não fiquem dúvidas, observe agora alguns exemplos de funções que não são do primeiro grau:
a) y = 2x2. Essa função não é do primeiro grau porque a variável independente possui grau 2. Nesse caso, ela é uma função do segundo grau.
b) y = 1/x. Essa função não é do primeiro grau porque y = 1/x também pode ser escrito como y = x-1 e esse (-1) não é o expoente correto para as funções do primeiro grau.
Gráfico da função do primeiro grau
Toda função do primeiro grau pode ser representada geometricamente por uma reta. Para construí-la, basta encontrar dois pares ordenados de pontos que pertencem a essa reta, colocá-los no plano cartesiano e traçar a reta que passa por eles. Tomando a função y = x – 3 como exemplo, o passo a passo da construção do gráfico de uma função do primeiro grau deve ser o seguinte:
1º Encontrar os pares ordenados
Para encontrá-los, basta escolher dois valores quaisquer para a variável independente e descobrir seus correspondentes por meio da função. Para isso, escolhemos x = 1 e x = 2 e construímos a tabela a seguir:
|
x |
y = x – 3 |
y |
Par ordenado (x,y) |
|
1 |
y = 1 – 3 = – 2 |
– 2 |
(1, –2) |
|
2 |
y = 2 – 3 = 0 |
– 1 |
(2, –1) |
A segunda coluna dessa tabela é preenchida com o valor de x substituído na função, a terceira com o valor final de y e a quarta com o par ordenado formado pelos valores de x e de y.
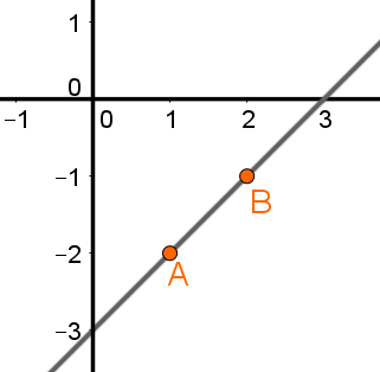
2º Colocar os pares ordenados no plano cartesiano e traçar a reta que os contém
Por Luiz Paulo Moreira
Graduado em Matemática