O que é o gráfico da função do 2° grau?

Uma função é uma regra que relaciona cada elemento de um conjunto A a um único elemento de um conjunto B. Geralmente, essa regra é conseguida por meio de uma expressão algébrica muito parecida com uma equação e, dependendo do grau dessa expressão algébrica e da quantidade de variáveis que ela possui, é possível construir seu gráfico.

Definição de gráfico

O gráfico de uma função é o conjunto de pontos (x, y) do plano cartesiano que satisfazem a seguinte condição: y = f(x). Em outras palavras, para cada valor de x, existe um único valor de y relativo a ele, obtido pela lei de formação da função.

Os gráficos mais importantes estudados no ensino fundamental pertencem à função do primeiro grau e do segundo grau. No ensino médio, também são estudados os gráficos da função logarítmica, exponencial, trigonométrica etc. Neste artigo, discutiremos uma técnica que pode ser usada para construir o gráfico de uma função do segundo grau.

Gráfico da função do segundo grau

Uma função do segundo grau é aquela que pode ser escrita da seguinte maneira:

f(x) = ax² + bx + c

Em que a, b e c são números reais, chamados coeficientes, com a sempre diferente de zero, e x é a variável independente.

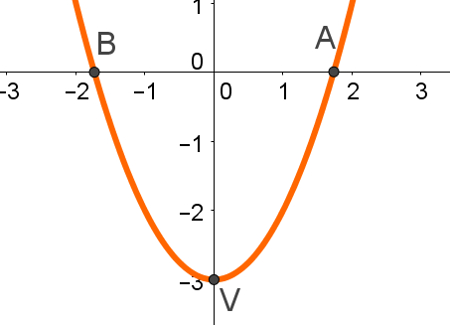
O gráfico dessas funções é sempre uma parábola que pode ser construída a partir de três pontos que pertencem a ela: vértice e as duas raízes, ou vértice e dois pontos “aleatórios”.

1 – Encontrando o vértice da parábola

As parábolas que podem ser usadas como gráfico de uma função do segundo grau devem ter sua concavidade voltada para cima ou para baixo. No primeiro caso, a parábola possui um ponto mais baixo, onde a função deixa de ser decrescente e passa a ser crescente. No segundo caso, a parábola possui um ponto mais alto, onde a função deixa de ser crescente e passa a ser decrescente. Esse ponto é chamado vértice.

Para encontrar as coordenadas do vértice V = (x_v, y_v), podemos usar as seguintes fórmulas:

x_v = – b  
         2a

e

y_v = – Δ  
         4a

2 – Encontrando as duas raízes da parábola

As raízes de uma função são os pontos nos quais o gráfico dessa função encontra o eixo x do plano cartesiano. No caso das funções do segundo grau, o número de raízes pode ser 0, 1 ou 2. Se a função possui duas raízes, o melhor a ser feito é usá-las na construção do gráfico.

Para encontrar as raízes de uma função do segundo grau, utilize a fórmula de Bháskara. Primeiro, determine o discriminante da função:

Δ = b² – 4ac

Em seguida, substitua-o na fórmula de Bháskara, assim como os coeficientes:

x = – b ± √?
          2a  

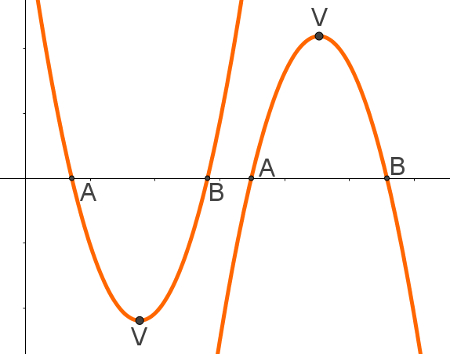
As coordenadas das raízes da função serão: A = (x’, 0) e B = (x’’, 0). A partir desses três pontos, as duas raízes e o vértice, basta colocá-los no plano cartesiano e ligá-los por meio de uma parábola. Nesse processo, note que a parábola terá a concavidade voltada para baixo se o vértice estiver acima do eixo x, ou terá a concavidade voltada para cima se o vértice estiver abaixo do eixo x.

Na imagem acima, observe que a primeira parábola possui vértice abaixo do eixo x e sua concavidade é voltada para cima. O inverso acontece à segunda parábola, que tem o vértice acima do eixo x e concavidade voltada para baixo.

Exemplo:

Construa o gráfico da função: f(x) = x² + 2x – 8.

O primeiro passo é encontrar o vértice dessa função. Usando as fórmulas estudadas, teremos:

x_v = – b  
        2a

x_v = – 2  
        2

x_v = – 1

y_v = – Δ  
         4a

y_v = – (b² – 4ac)
          4a

y_v = – (2² – 4·1·[– 8])
           4

y_v = – (4 + 32)
         4

y_v = – (4 + 32)
          4

y_v = – (36)  
           4

y_v = – 9

Assim, as coordenadas do vértice dessa parábola são: V = (– 1, –9).

Observe que já sabemos o valor do discriminante dessa função, que foi feito para encontrar y_v. Δ = 36. Usando a fórmula de Bháskara para encontrar as raízes, teremos:

x = – b ± √?
         2a

x = – 2 ± √36
         2

x = – 2 ± 6
         2

x’ = – 2 – 6 = – 8   = – 4
 2          2

x’’ = – 2 + 6 =   4   = 2
     2          2

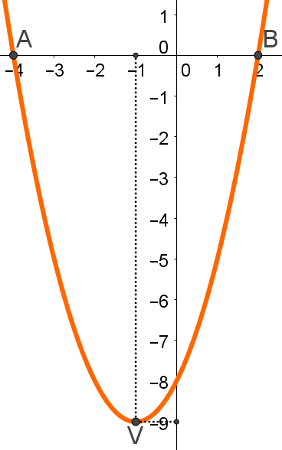
Então, as raízes podem ser encontradas nos pontos: A = (– 4, 0) e B = (2, 0). Marcando esses três pontos no plano cartesiano, e depois construindo a parábola que passa por eles, teremos:

Vértice + pontos aleatórios

Essa construção é válida quando a função possui duas raízes reais e distintas, ou seja, quando ? > 0. Quando a função possui apenas uma raiz real, ou não possui nenhuma, não faz sentido tentar encontrar suas raízes para construir seu gráfico.

Nesse caso, encontraremos primeiro as coordenadas do vértice, depois, dado x_v a coordenada x do vértice, escolheremos os valores x_v + 1 e x_v – 1 como pontos “aleatórios” e descobriremos o valor de y relacionado a cada um desses pontos. Os resultados disso serão os pontos V, A e B, exatamente como feito nas raízes, com a diferença de que os pontos A e B não estão mais sobre o eixo x.

Por exemplo, construa o gráfico da função: f(x) = x² + 4.

Essa função não possui raízes, pois o valor de ? é menor que zero. Nesse caso, encontraremos as coordenadas do vértice e calcularemos os pontos “aleatórios”, propostos anteriormente:

x_v = – b  
         2a

x_v = – 0  
         2

x_v = 0

y_v = – Δ  
         4a

y_v = – (b² – 4ac)
          4a

y_v = – (0² – 4·1·4)
          4

y_v = – (– 16)
           4

y_v = 16
        4

y_v = 4

Assim, V = (0, 4).

Tomando x_v = 0, faremos: x_v + 1 = 0 + 1 = 1. Substituindo esse valor na função, para encontrar y relativo a ele, teremos:

f(x) = x² + 4

f(1) = 1² + 4

f(1) = 5

Portanto, o ponto A será: A = (1, 5).

Tomando x_v = 0, também faremos: x_v – 1 = 0 – 1 = – 1. Portanto:

f(x) = x² + 4

f(– 1) = (– 1)² + 4

f(– 1) = 1 + 4

f(– 1) = 5

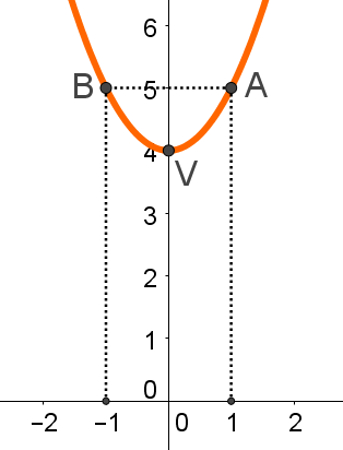
Portanto, o ponto B será: B = (– 1, 5).

Assim, o gráfico dessa função será:

Por Luiz Paulo Moreira
Graduado em Matemática