Toda função, independente do seu grau, possui um gráfico e cada um é representado de uma forma diferente. O gráfico de uma função de 1º grau é uma reta que poderá ser crescente ou decrescente. O gráfico de uma função de 2º grau será uma parábola de concavidade para baixo ou para cima.
Toda função do 2º grau é formada a partir da forma geral f(x) = ax2 + bx + c, com
a ≠ 0.
No primeiro momento, para construir um gráfico de uma função de 2º grau qualquer, basta atribuir valores para x e encontrar valores correspondentes para a função. Portanto, formaremos pares ordenados, com eles iremos construir o gráfico, veja alguns exemplos:
Exemplo 1:
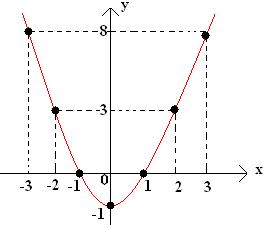
Dada a função f(x) = x2 – 1. Essa função pode ser escrita da seguinte forma: y = x2 – 1.
Atribuiremos qualquer valor para x e substituindo na função encontraremos o valor de y, formando pares ordenados.
y = (-3)2 – 1
y = 9 – 1
y = 8
(-3,8)
y = (-2)2 – 1
y = 4 – 1
y = 3
(-2,3)
y = (-1)2 – 1
y = 1 – 1
y = 0
(-1,0)
y = 02 – 1
y = -1
(0,-1)
y = 12 – 1
y = 1 – 1
y = 0
(1,0)
y = 22 – 1
y = 4 – 1
y = 3
(2,3)
y = 32 – 1
y = 9 – 1
y = 8
(3,8)
Distribuindo os pares ordenados no plano cartesiano montaremos o gráfico.
O gráfico desse exemplo tem a concavidade voltada para cima, podemos relacionar a concavidade com o valor do coeficiente a, quando a > 0 a concavidade sempre será voltada para cima.
Exemplo 2:
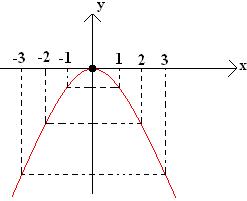
Dada a função f(x) = -x2. Atribuiremos qualquer valor para x e substituindo na função encontraremos o valor de y, formando pares ordenados.
y = -(-3)2
y = - 9
(-3,-9)
y = -(-2)2
y = - 4
(-2,-4)
y = -(-1)2
y = -1
(-1,-1)
y = -(0)2
y = 0
(0,0)
y = -(1)2
y = -1
(1,-1)
y = -(2)2
y = -4
(2,-4)
y = -(3)2
y = -9
(3,-9)
Distribuindo os pares ordenados no plano cartesiano montaremos o gráfico.
O gráfico do exemplo 2 tem a concavidade voltada para baixo, como já foi dito na conclusão do exemplo 1 que a concavidade está relacionada com o valor do coeficiente a, quando a < 0 a concavidade sempre será voltada para baixo.
Por Danielle de Miranda
Graduada em Matemática
Equipe Brasil Escola