Gráfico da função de 2º grau

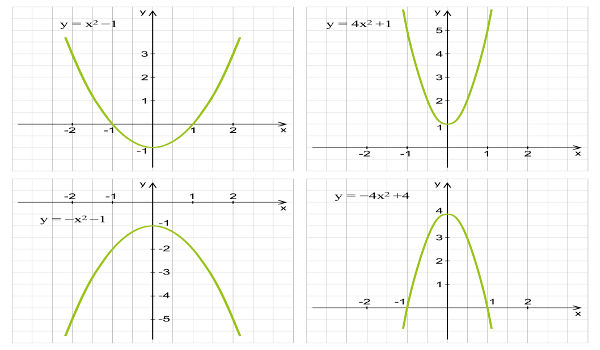
Uma função do 2º grau é definida pela seguinte lei de formação f(x) = ax² + bx + c ou y = ax² + bx + c, em que a, b e c são números reais e a ≠ 0. Sua representação no plano cartesiano é uma parábola que, de acordo com o valor do coeficiente a, possui concavidade voltada para cima ou para baixo. A função do 2º grau assume três possibilidades de resultados ou raízes, que são determinadas quando fazemos f(x) ou y igual a zero, transformando a função em uma equação do 2º grau, que pode vir a ser resolvida por Bháskara.

Tópicos deste artigo

• 1 - Gráfico da função do 2º grau

Gráfico da função do 2º grau

Coeficiente a > 0, parábola com a concavidade voltada para cima
Coeficiente a < 0, parábola com a concavidade voltada para baixo

? > 0 – A equação do 2º grau possui duas soluções distintas, isto é, a função do 2º grau terá duas raízes reais e distintas. A parábola intersecta o eixo das abscissas (x) em dois pontos.

? = 0 – A equação do 2º grau possui uma única solução, isto é, a função do 2º grau terá apenas uma raiz real. A parábola irá intersectar o eixo das abscissas (x) em apenas um ponto.

? < 0 – A equação do 2º grau não possui soluções reais, portanto, a função do 2º grau não intersectará o eixo das abscissas (x).

Pontos notáveis do gráfico de uma função do 2º grau

O vértice da parábola constitui um ponto importante do gráfico, pois indica o ponto de valor máximo e o ponto de valor mínimo. De acordo com o valor do coeficiente a, os pontos serão definidos, observe:

Quando o valor do coeficiente a for menor que zero, a parábola possuirá valor máximo.

Quando o valor do coeficiente a for maior que zero, a parábola possuirá valor mínimo.

Outra relação importante na função do 2º grau é o ponto onde a parábola corta o eixo y. Verifica-se que o valor do coeficiente c na lei de formação da função corresponde ao valor do eixo y onde a parábola o intersecta.

Por Marcos Noé
Graduado em Matemática