As figuras geométricas planas conhecidas como cônicas são formadas pela intersecção entre um plano e um cone duplo de revolução. São elas: circunferência, parábola, hipérbole e elipse.
O cone duplo de revolução é um sólido geométrico tridimensional obtido por meio do giro de uma reta. A figura formada por esse giro, ou seja, o cone duplo de revolução, é representada a seguir:
Cada um dos quatro tipos de figuras formados pela intersecção do plano com o cone está relacionado a um tipo de equação, portanto, essas figuras também podem ser definidas de forma algébrica. Tanto a definição de cada uma delas quanto suas respectivas equações serão discutidas no decorrer deste artigo.
Tópicos deste artigo
Circunferência
As circunferências podem ser obtidas por meio da intersecção de um plano com um cone. A definição delas é: dado um ponto C, chamado de centro, e um comprimento r, chamado de raio, a circunferência é o conjunto de pontos do plano cuja distância até C é sempre igual a r.
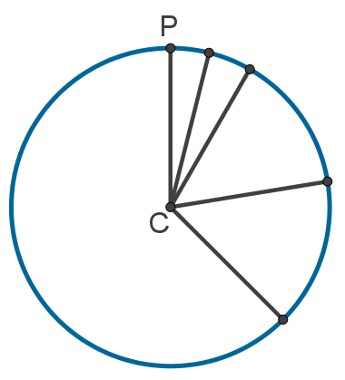
A imagem a seguir mostra um exemplo de circunferência com alguns de seus raios. Note que, de acordo com a definição dada, todos os segmentos de reta cujas extremidades são o centro e qualquer ponto da circunferência possuem a mesma medida.
A equação reduzida da circunferência também pode ser obtida usando a distância entre dois pontos. Dados os pontos C (a, b), centro da circunferência, e P (x, y) ponto qualquer pertencente a ela, a equação reduzida da circunferência é:
(x – a)2 + (y – b)2 = r2
Elipse
Em uma elipse, os pontos F1 e F2 são chamados de focos, e a distância entre eles é igual a 2c. Sua definição formal é: dados os pontos F1 e F2, a elipse é o conjunto de pontos P em que vale a seguinte expressão:
dPF1 + dPF2 = 2a
Isso significa que a elipse é o conjunto dos pontos cuja soma das distâncias até os focos é igual a uma constante. Em outras palavras, o ponto P pertence a uma elipse se a soma da distância de P até F1 com a distância de P até F2 é igual a 2a.
A figura a seguir ilustra uma elipse com as medidas de segmentos importantes encontrados nela:
As elipses possuem duas equações reduzidas. A primeira delas é válida para o caso em que os focos dessa figura estão sobre o eixo x e o centro da elipse coincide com a origem de um plano cartesiano:
x 2+ y 2= 1
a2 b2
A segunda equação reduzida é válida para os casos em que os vértices da elipse estão sobre o eixo y e seu centro sobre a origem do plano cartesiano.
y 2+ x2 = 1
a2 b2
Parábola
Dada uma reta r e um foco F, a parábola é a cônica na qual todos os seus pontos têm a distância até r igual à distância até F.
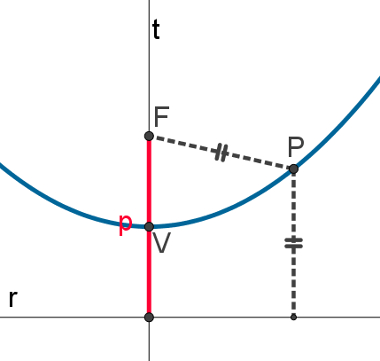
A figura a seguir mostra um exemplo de parábola com o ponto P, em que vale:
dPF = dPr
Toda parábola possui um eixo de simetria, que é a reta “t” na imagem acima. Quando esse eixo coincide com o eixo x do plano cartesiano e o vértice da parábola coincide com a origem do plano cartesiano, a equação reduzida da parábola é:
y2 = 2px
Quando o eixo de simetria está sobre o eixo y e o vértice da parábola coincide com a origem do plano cartesiano, a equação reduzida da parábola é:
x2 = 2py
Hipérbole
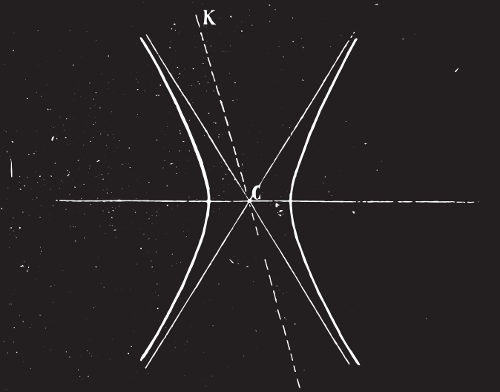
Dados os pontos F1 e F2, chamados de focos da hipérbole, e a distância 2c entre eles, uma hipérbole é o conjunto de pontos do plano cuja diferença das distâncias até os focos é igual à constante 2a.
Assim, se P é um ponto da hipérbole, vale a expressão:
|dPF1 – dPF2| = 2a
A imagem a seguir mostra um exemplo de hipérbole e alguns segmentos importantes em sua formação:
As equações reduzidas da hipérbole também são duas. A primeira é obtida quando os focos dessa figura estão sobre o eixo x e seu centro coincide com a origem do plano cartesiano:
x 2 – y 2= 1
a2 b2
A segunda é obtida quando os focos da hipérbole estão sobre o eixo y e seu centro coincide com a origem do plano cartesiano:
y 2 – x 2= 1
a2 b2
Por Luiz Paulo Moreira
Graduado em Matemática
.jpg)
.jpg)
.jpg)