O que são cônicas?

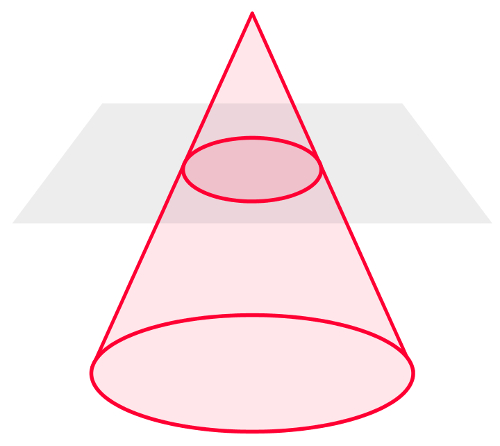
Cônicas são figuras geométricas planas definidas a partir da intersecção de um cone duplo de revolução com um plano. As figuras que podem ser obtidas nessa intersecção, e que podem ser chamadas de cônicas, são: circunferência, elipse, parábola e hipérbole.

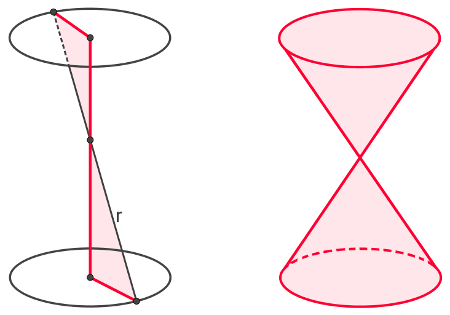
O cone duplo de revolução é conseguido com o giro de uma reta r sobre um eixo, que, por sua vez, é outra reta concorrente à reta r. A imagem a seguir mostra a reta que foi girada, o eixo e a figura obtida a partir dessa revolução.

Todas as definições das cônicas são baseadas na distância entre dois pontos, que pode ser encontrado no plano por meio do teorema de Pitágoras.

Tópicos deste artigo

• 1 - Circunferência
• 2 - Elipse
• 3 - Parábola
• 4 - Hipérbole

Circunferência

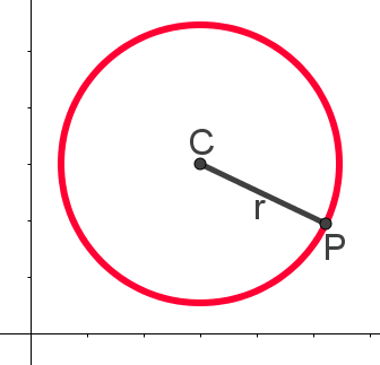
Dado um ponto C e um comprimento fixo r, todo ponto que está a uma distância r do ponto C é um ponto da circunferência. O ponto C é chamado de centro da circunferência e r é seu raio. A seguinte imagem mostra um exemplo de circunferência e a forma que ela assume no plano cartesiano:

Dadas as coordenadas do ponto C (a, b), as coordenadas do ponto P (x, y) e o comprimento do segmento r, a equação reduzida da circunferência é:

(x – a)² + (y – b)² = r²

Elipse

Dados dois pontos F₁ e F₂ do plano, chamados de focos, a elipse é o conjunto dos pontos P, tais que a soma da distância de P a F₁ com a distância de P a F₂ é a constante 2a. A distância entre os pontos F₁ e F₂ é 2c e 2a > 2c.

Comparando as definições de elipse e circunferência, na elipse, somamos as distâncias que vão de um ponto da elipse até seus focos e observamos o resultado constante. Na circunferência, apenas uma distância é constante.

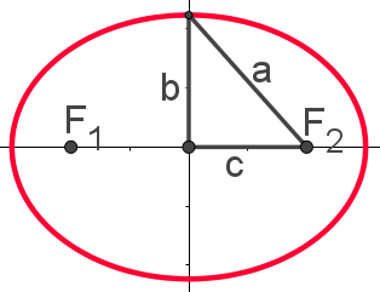
A imagem a seguir mostra um exemplo de elipse e a forma dessa figura no plano cartesiano:

Nessa figura, pode-se observar os segmentos a, b e c, que serão usados para determinar as equações reduzidas da elipse.

Existem duas versões da equação reduzida da elipse; a primeira é válida para quando os focos estão sobre o eixo x de um plano cartesiano e o centro da elipse coincide com a origem:

 x² +  y² = 1
 a²     b²       

A segunda versão é válida para quando os focos estão sobre o eixo y e o centro da elipse coincide com a origem:

 y² +  x² = 1
 a²     b²       

Parábola

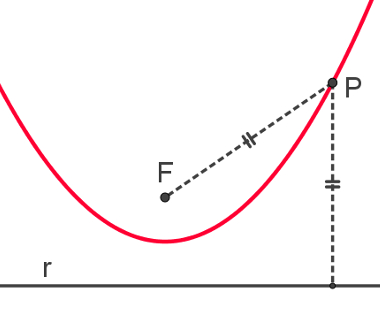
Dada uma reta r, chamada de diretriz, e um ponto F, chamado de foco, ambos pertencentes ao mesmo plano, uma parábola é o conjunto de pontos P, tais que a distância entre P e F seja igual à distância entre P e r.

A figura a seguir mostra um exemplo de parábola:

O parâmetro de uma parábola é a distância entre o foco e a diretriz, e essa medida é representada pela letra p. Também existem duas versões para a equação reduzida da parábola. A primeira é válida quando o foco está sobre o eixo x:

y² = 2px

A segunda é válida quando o foco está sobre o eixo y:

x² = 2py

Hipérbole

Dados dois pontos distintos F₁ e F₂, chamados de focos, de um plano qualquer, e a distância 2c entre esses pontos, um ponto P pertencerá à hipérbole se a diferença entre a distância de P até F₁ e a distância de P a F₂, em módulo, for igual a uma constante 2a. Assim:

|PF₁ – PF₂| = 2a

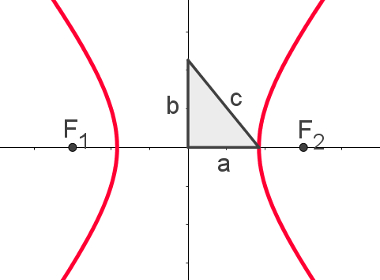
A imagem a seguir é uma hipérbole com os segmentos a, b e c.

A hipérbole também possui duas versões de equação reduzida. A primeira é referente aos casos em que os pontos F₁ e F₂ estão sobre o eixo x e o centro da hipérbole é a origem do plano cartesiano.

 x² -  y² = 1
 a²     b²       

O segundo caso é para quando os focos da hipérbole estão sobre o eixo y e seu centro coincide com a origem do plano cartesiano.

 y² -  x² = 1
 a²     b²       

Por Luiz Paulo Moreira
Professor de Matemática