Área de uma região triangular através do determinante

Bem, sabemos que os elementos que fundamentam a geometria analítica são os pontos e suas coordenadas, já que através destes podemos calcular distâncias, coeficientes angulares das retas e áreas de figuras planas.

Dentre os cálculos das áreas de figuras planas, existe uma expressão que determina a área de uma região triangular utilizando apenas as coordenadas dos vértices do triângulo.

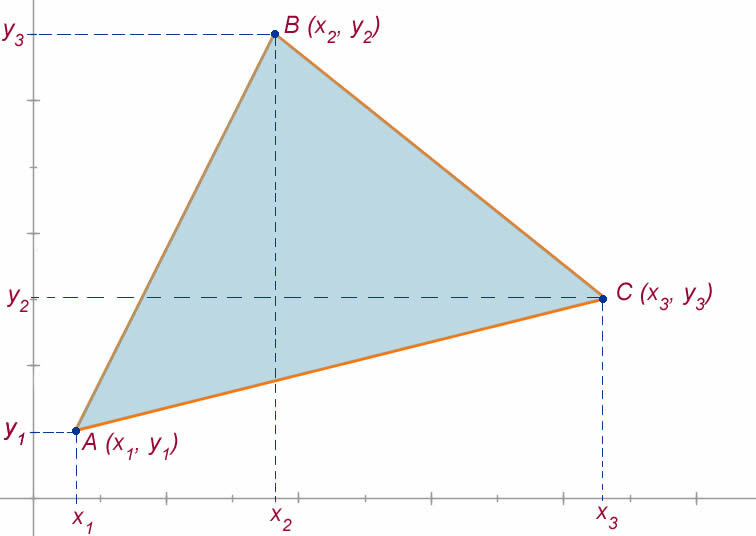
Portanto, consideremos um triângulo com vértices de coordenadas quaisquer e assim vejamos como calcular a área desse triângulo apenas com as coordenadas dos seus vértices.

O parâmetro D é determinado pela matriz das coordenadas dos vértices do triângulo ABC.

Note que o parâmetro D é a mesma matriz determinante para verificar a condição de alinhamento de três pontos (ver Condição de alinhamento de três pontos).

Assim sendo, caso você verifique a área de um suposto triângulo e o determinante dê zero, saiba que na verdade esses três pontos não constituem um triângulo, pois estão alinhados (por isso a área é zero).

Uma observação importante em relação à expressão para o cálculo da área é quanto ao Parâmetro D estar em módulo, ou seja, usaremos o seu valor absoluto. Por se tratar de área, não devemos adotar um determinante negativo, pois isso resultará em uma área negativa e isso não existe.

Vejamos um exemplo para uma melhor compreensão:

“Determine a área da região triangular que tem como vértices os pontos A (4,0), B (0,0) e C (2,2)”.

Portanto, a área da região triangular do triângulo ABC é de 4 u.a (unidades de área).

Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe BrasilEscola