Função linear

Função linear é o caso particular de função do 1° grau quando b = 0 . Assim, a forma geral de uma função linear é \(f\left(x\right)=ax\). O gráfico de uma função linear é uma reta que passa pela origem, que é o ponto (0,0).

Leia também: Funções — o que são, tipos, exemplos

Tópicos deste artigo

• 1 - Resumo sobre função linear
• 2 - Videoaula sobre função linear
• 3 - O que é função linear?
• 4 - Gráfico da função linear
• 5 - Tipos de função linear
  • Função nula
  • Função crescente
  • Função decrescente
• 6 - Função linear no cotidiano
• 7 - Exercícios resolvidos sobre função linear

Resumo sobre função linear

• Uma função do 1° grau na forma \(f\left(x\right)=ax\), com coeficiente a  real, é chamada de função linear.
• Em uma função linear, \(f\left(0\right)=0\). Portanto, o gráfico de toda função real cruza o ponto (0,0).
• Se a = 0, a função linear também é chamada de função nula, pois, para todo x  real, \(f\left(x\right)=0\).
• Se a > 0, a função linear é crescente.
• Se a < 0, a função linear é decrescente.

Videoaula sobre função linear

O que é função linear?

Uma função do 1° grau é descrita pela lei \(f\left(x\right)=ax+b\), em que a e b são constantes reais, e a variável x é real. Se b = 0, então a função é descrita pela lei \(f\left(x\right)=ax\) e é chamada de função linear. Portanto, a função linear é um caso específico de função do 1° grau.

Exemplos:

\(f\left(x\right)=2x\)

\(g\left(x\right)=-7x\)

\(h\left(x\right)=\frac{1}{3}x\)

\(i\left(x\right)=\pi x\)

[Publicidade_omnia]

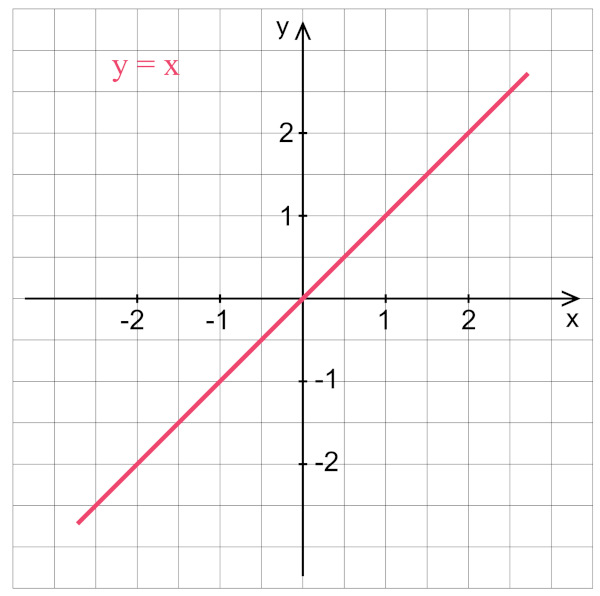
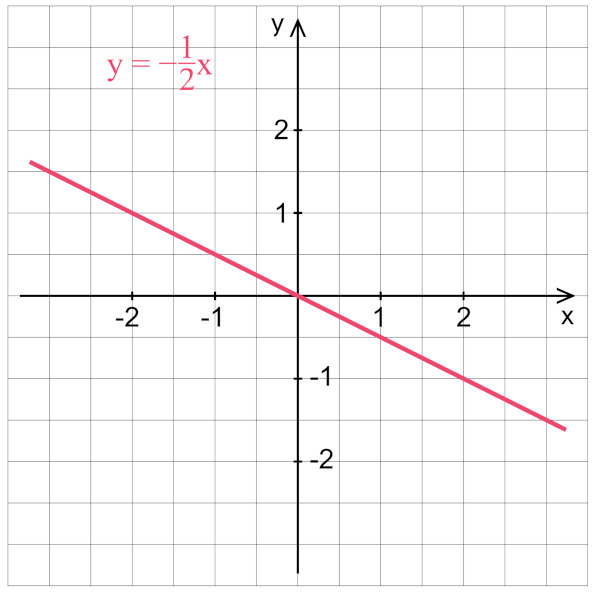
Gráfico da função linear

Como a função linear é uma função do 1° grau, seu gráfico é sempre uma reta. Ainda, como a forma geral da função linear é \(f\left(x\right)=ax\), temos que, quando x = 0,

\(f\left(0\right)=a\cdot0=0\)

Ou seja, o ponto (0,0) sempre pertence a uma função linear. Logo, o gráfico da função linear sempre passa pela origem.

Exemplos:

Tipos de função linear

• Função nula

Uma função linear com = 0 é uma função em que, para qualquer valor de x, a imagem é zero:

\(f\left(x\right)=0\cdot x=0\)

A função \(f\left(x\right)=0\) é chamada de função nula e seu gráfico é uma reta que coincide com o eixo x .

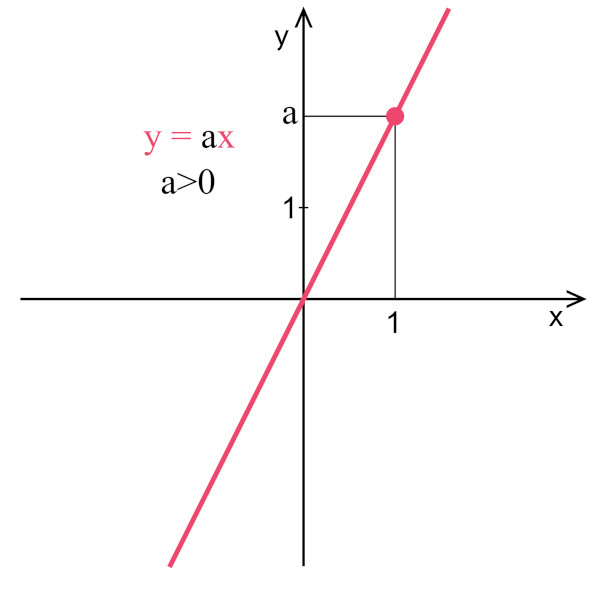
• Função crescente

Uma função linear com a > 0 é uma função em que, para valores crescentes de x, a imagem é crescente.

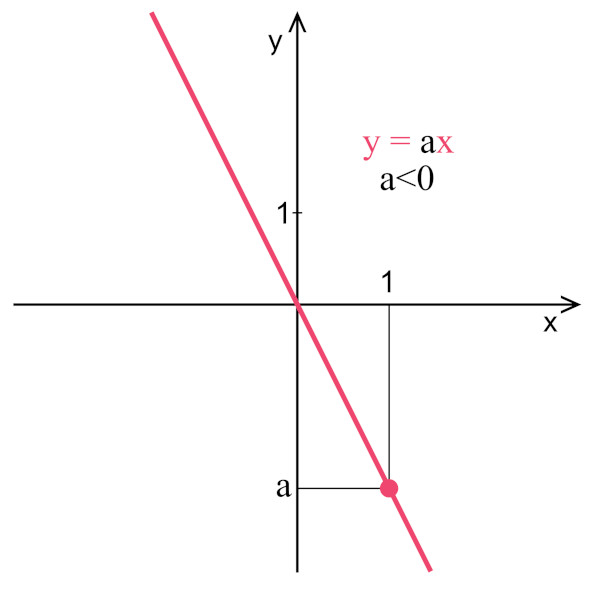
• Função decrescente

Uma função linear com a < 0 é uma função em que, para valores crescentes de x, a imagem é decrescente.

Função linear no cotidiano

Assim como outras funções do 1° grau, a função linear pode ser utilizada para descrever situações do cotidiano.

Exemplo: Um produto custa x reais a unidade e Ana pretende comprar a unidades. Qual função linear descreve o gasto total da compra de Ana?

Se Ana comprar 1 unidade, o gasto será x reais.

Se comprar 2 unidades, o gasto será 2x reais.

Se comprar 3 unidades, o gasto será 3x reais.

...

Se comprar a  unidades, o gasto será ax reais.

Portanto, \(f\left(x\right)=ax\) é a função que descreve o gasto total de Ana a partir da compra de a unidades de um produto que custa x reais a unidade.

Leia também: Sinais de uma função do 1º grau

Exercícios resolvidos sobre função linear

Questão 1

Considere as afirmações sobre a função \(f\left(x\right)=3x\).

I. O gráfico da função é uma reta.

II. Para cada valor de x, a respectiva imagem \(f\left(x\right)\) é o triplo.

III. O gráfico da função cruza o ponto (2,3).

Está correto o que se afirma em:

a) I, apenas.

b) II, apenas.

c) III, apenas.

d) I e II, apenas.

e) I, II e III.

Resolução

I. Verdadeira.

II. Verdadeira.

III. Falsa, pois \(f\left(2\right)=3\cdot2=6\), ou seja, o gráfico cruza o ponto (2,6), mas não o ponto (2,3).

Alternativa D.

Questão 2

Seja \(g\left(x\right)=-x\). Em relação às características de g, é correto afirmar que:

a) o gráfico dessa função é uma parábola.

b) \(g\left(0\right)=-1\).

c) essa função é crescente.

d) o ponto (1,-1) pertence ao gráfico de g.

e) o gráfico dessa função não cruza o eixo das abcissas.

Resolução

Como \(g\left(x\right)=-x\) é uma função linear, seu gráfico é uma reta que cruza a origem (ou seja, cruza o eixo das abcissas no ponto (0,0)). Além disso, como a < 0,  pois a = -1, tem-se que a função é decrescente. Por fim, \(g\left(1\right)=-1\), ou seja, o ponto (1,-1)  pertence ao gráfico de g.

Alternativa D.

Fontes:

GUIDORIZZI, H.L. Um curso de cálculo. 5. ed. Rio de Janeiro: LTC, 2001. v.1.

LIMA, Elon L. et al. A Matemática do Ensino Médio. 11. ed. Coleção Professor de Matemática. Rio de Janeiro: SBM, 2016. v.1.