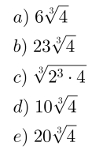Antes de partir para o cálculo de raízes não exatas propriamente dito, é necessário relembrar como calcular raízes de um modo geral e o que são raízes exatas e não exatas.
Calculando raízes
Calcular a raiz de um número resume-se a procurar por outro número que, multiplicado por ele mesmo determinada quantidade de vezes, tenha como resultado o número dado.
A representação de raízes é feita da seguinte maneira:
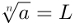
*n, chamado de índice, é o número de fatores da potência que gerou a, chamado de radicando, e L é o resultado, chamado de raiz.
Desse modo, L é um número que foi multiplicado por si mesmo n vezes e o resultado dessa multiplicação foi a.
L·L·L·L...L·L = a
Raízes exatas e não exatas
Dizemos que uma raiz é exata quando L é um número inteiro. São alguns exemplos de raízes exatas:
a) A raiz quadrada de 9, pois 3·3 = 9
b) A raiz cúbica de 8, pois 2·2·2 = 8
c) A raiz quarta de 16, pois 2·2·2·2 = 16
Entretanto, quando não é possível encontrar número inteiro que seja raiz de um número, então, essa raiz não é exata. Todas elas pertencem ao conjunto dos números irracionais e, por isso, todas elas são decimais infinitos. São alguns exemplos de raízes não exatas:
a) Raiz quadrada de 2
b) Raiz cúbica de 3
c) Raiz quarta de 5
Cálculo de raízes não exatas
Caso 1 – Radicando primo
Se o radicando pertence ao conjunto dos números primos, é preciso procurar por valores aproximados para sua raiz. Esse cálculo é feito procurando-se por raízes exatas próximas ao radicando e, posteriormente, aproximando a raiz do radicando tendo como base a raiz exata mais próxima. Por exemplo, calculemos a raiz cúbica de 31:
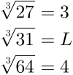
Na imagem anterior, vimos que a raiz cúbica de 31 tem um resultado decimal entre 3 e 4. Para descobrir uma aproximação de L, é necessário definir quantas casas decimais ele deve ter e procurar pelo número que, elevado ao cubo, mais se aproxime de 31. No exemplo, usaremos uma aproximação com duas casas decimais. Portanto, L = 3,14, pois:
3,143 = 30,959144
Caso 2 – Radicando não primo
Quando o radicando não é primo, decomponha-o em fatores primos e agrupe esses fatores em potências cujo expoente seja igual ao índice do radicando. Isso permitirá o cálculo imediato de todos os fatores cujo expoente é igual ao índice e resumirá os cálculos às raízes dos menores números primos possíveis para aquela raiz.
Exemplo:
Sabendo que a raiz cúbica de 2 é aproximadamente 1,26, calcule a raiz cúbica de 256. Em outras palavras, calcule:
Solução: Primeiramente, obtenha a decomposição em fatores primos de 256:
256|2
128|2
64|2
32|2
16|2
8|2
4|2
2|2
1
256 = 23·23·22
Agora, reagrupe os fatores em potências de expoente 3 dentro do radical. Observe:
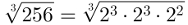
Por fim, é possível utilizar uma das propriedades dos radicais para simplificar a raiz acima. Portanto, reescreva a igualdade da seguinte maneira para obter o resultado indicado:
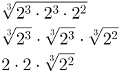
Para encontrar o valor numérico da expressão acima, note que o resultado traz uma raiz cúbica de 2 elevado ao quadrado. Podemos reescrever da seguinte maneira:
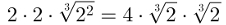
Substitua as raízes cúbicas de 2 pelo valor dado no exercício e realize a multiplicação.
4·1,26·1,26 = 6,35
Por Luiz Paulo Moreira
Graduado em Matemática