Pontos, retas, planos e o espaço são noções primitivas para a Matemática. Assim, temos uma boa noção sobre o que esses objetos são e de seus formatos, mas não é possível defini-los. Neste texto, vamos estudar o plano.
O que é plano?
O plano é um conjunto de retas dispostas lado a lado de modo que não haja espaços entre essas retas e que ele também seja infinito, além de não descrever qualquer curva.
Ideia gráfica de uma parte da reta à esquerda e da parte de um plano à direita
Planos em postulados
Postulado (ou axioma) é um fato que dispensa demonstração para ser aceito como verdade. A única garantia de que pontos, retas e planos existem são os postulados de existência. No caso específico do plano, esse postulado é:
“Existe plano. Nele e fora dele existem pontos.”
Para construir um plano, existe um postulado de determinação:
“Três pontos não colineares determinam um plano único que os contém.”
Como obter planos?
Os planos podem ser obtidos de algumas maneiras diferentes.
Por meio do postulado de determinação
Para tanto, basta observar que três pontos não colineares determinam um plano único. Logo, obter três pontos não colineares é um dos meios de se obter um plano.
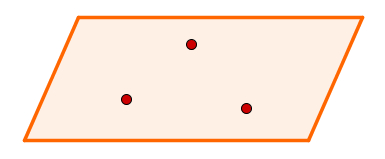
Plano determinado por três pontos distintos não colineares
Por meio de uma reta e de um ponto fora dela
Três pontos não colineares determinam um plano. Sendo assim, tome dois pontos distintos na reta e o ponto fora dela e terá os três pontos de que precisa para determinar o plano.
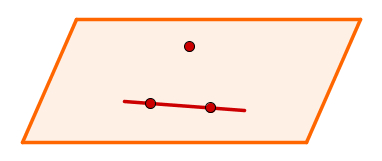
Plano determinado por uma reta e um ponto fora dela
Por meio de duas retas concorrentes
Tendo em vista que duas retas concorrentes encontram-se em um ponto A, tome outros dois pontos, um em cada reta. Esses dois últimos pontos e o ponto A não são colineares e isso determina o plano.
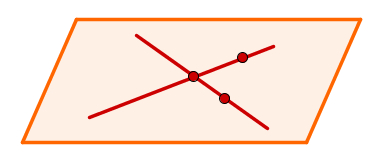
Plano determinado por duas retas concorrentes
Por meio de duas retas paralelas não coincidentes
Tome dois pontos distintos em uma das retas e um ponto na outra. Isso evidenciará três pontos não colineares que são suficientes para determinar um plano.
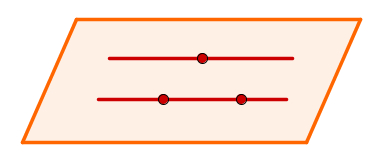
Plano determinado por duas retas paralelas não coincidentes
Por Luiz Paulo Moreira
Graduado em Matemática
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SILVA, Luiz Paulo Moreira. "O que é plano?"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-plano.htm. Acesso em 05 de julho de 2020.
