O que são posições relativas?

As posições relativas entre duas figuras geométricas constituem o estudo das possibilidades de interação entre esses elementos no espaço em que ocupam. Em outras palavras, as figuras são classificadas de acordo com o número ou com a forma como as interações entre elas ocorrem. As posições relativas triviais, por exemplo, acontecem entre ponto e reta, que são apenas duas: um ponto pertence a uma reta ou não pertence a ela.

Tópicos deste artigo

• 1 - Posições relativas entre duas retas
• 2 - Posições relativas entre reta e plano
• 3 - Posições relativas entre planos
• 4 - Posições relativas entre um ponto e uma circunferência
• 5 - Posições relativas entre reta e circunferência
• 6 - Posições relativas entre duas circunferências

Posições relativas entre duas retas

1 – Retas paralelas: Duas retas são paralelas quando não possuem ponto em comum. Lembrando que isso vale para toda a extensão dessas retas e que elas são infinitas.

2 – Retas concorrentes: Duas retas são concorrentes quando possuem um único ponto em comum. Quando o ângulo formado entre essas duas retas é de 90°, dizemos que elas são perpendiculares.

3 – Retas coincidentes: Duas retas são coincidentes quando possuem dois ou mais pontos em comum. É possível mostrar que, se as retas r e s possuem dois (ou mais) pontos em comum, então r = s. Por isso, retas coincidentes são vistas como uma única reta, ou como duas retas distintas que ocupam o mesmo espaço.

Posições relativas entre reta e plano

1 – Reta e plano paralelos: uma reta é paralela a um plano quando eles não possuem nenhum ponto em comum.

2 – Reta e plano concorrentes: uma reta r é concorrente a um plano α quando eles possuem um único ponto P em comum. Se por P passa, pelo menos, duas retas distintas contidas no plano α, cada uma delas perpendicular à reta r, então a reta r é perpendicular ao plano α.

3 – Reta contida no plano: uma reta é contida em um plano quando todos os seus pontos também são pontos do plano.

Posições relativas entre planos

1 – Planos paralelos: dois planos são paralelos quando não há ponto de encontro entre eles.

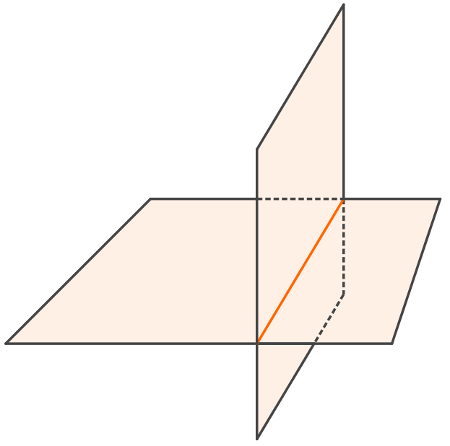
2 – Planos concorrentes: dois planos são concorrentes quando se intersectam. A intersecção entre dois planos é igual a uma reta.

3 – Planos coincidentes: dois planos são coincidentes quando todos os pontos do primeiro plano também são pontos do segundo.

A imagem a seguir mostra a intersecção de dois planos concorrentes.

Dois planos são perpendiculares quando um deles contém uma reta perpendicular ao outro plano.

Posições relativas entre um ponto e uma circunferência

Dada uma circunferência c, de centro O e raio r, e um ponto P, teremos as seguintes posições relativas:

1 – Ponto interno: o ponto P pertence à região interna da circunferência sempre que a distância entre P e o centro O da circunferência é menor que o raio r. Em outras palavras, sempre que d_OP < r.

2 – Ponto pertencente à circunferência: o ponto P pertence à circunferência c sempre que d_OP = r.

3 – Ponto exterior: um ponto P pertence à região externa da circunferência c sempre que d_OP > r.

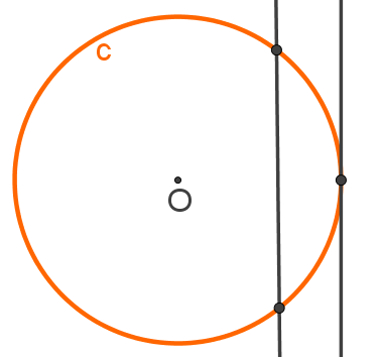
Posições relativas entre reta e circunferência

1 – Reta externa: a reta e a circunferência não possuem ponto em comum.

2 – Reta tangente: a reta e a circunferência possuem apenas um ponto em comum.

3 – Reta secante: a reta e a circunferência possuem dois pontos em comum.

A imagem a seguir mostra como são uma reta tangente e uma reta secante à circunferência.

Posições relativas entre duas circunferências

1 – Circunferências disjuntas

a) Disjuntas internas: as circunferências não possuem ponto em comum, e todos os pontos de uma delas ficam na região interior da outra.
b) Disjuntas externas: As circunferências não possuem ponto em comum, e todos os pontos de uma delas ficam na região exterior da outra.

2 – Circunferências tangentes

a) Tangentes internas: as circunferências possuem apenas um ponto em comum e todos os outros pontos de uma delas ficam na região interna da outra.
b) Tangentes externas: as circunferências possuem apenas um ponto em comum e todos os outros pontos de uma delas ficam na região externa da outra.

3 – Circunferências secantes: as circunferências possuem dois pontos em comum.