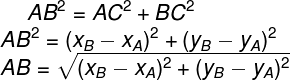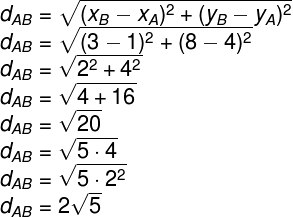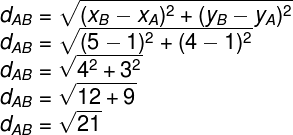O que é distância entre dois pontos?

A distância entre dois pontos pode ser obtida calculando ou medindo o comprimento do segmento de reta que os liga. Para calcular seu comprimento, podemos fazer uso da Geometria Analítica e encontrar uma fórmula capaz de determinar a distância entre dois pontos usando suas coordenadas. Considerando os pontos A (x_A, y_A) e B(x_B, y_B), essa fórmula assume a seguinte forma:

Demonstração

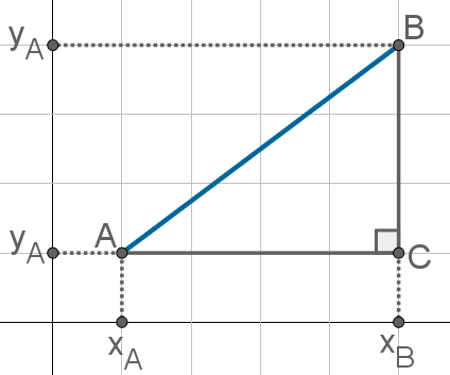
Para demonstrar essa fórmula, precisamos marcar os pontos A(x_A, y_A) e B(x_B, y_B) no plano cartesiano. Feito isso, construa o segmento de reta que os liga. Lembre-se de que a distância entre dois pontos é a menor distância entre eles.

Na figura acima, marcamos os pontos A e B e destacamos suas coordenadas nos eixos x e y. Observe que, para marcar essas coordenadas, acabamos construindo o triângulo ABC, que é retângulo e cuja hipotenusa é o segmento AB. Dessa forma, poderemos usar o teorema de Pitágoras para encontrar o comprimento desse segmento.

Antes disso, porém, é preciso conhecer o comprimento dos segmentos AC e BC, que são os catetos desse triângulo. O segmento AC mede x_B – x_A, já o segmento BC mede y_B – y_A. No teorema de Pitágoras, teremos:

Como o comprimento do segmento AB é justamente a distância entre os pontos A e B, concluímos que:

Exemplos:

1º Exemplo – Determine a distância entre os pontos A(2, 4) e B(3, 8).

Solução: Usando a fórmula da distância entre dois pontos, teremos:

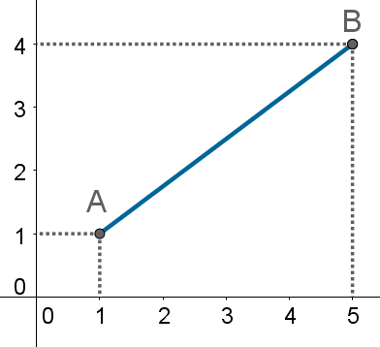
2º Exemplo – Determine o comprimento do segmento de reta da imagem a seguir:

Solução: Observe que as coordenadas dos pontos são: A(1, 1) e B(5, 4). Assim, basta usar a fórmula para determinar a distância entre os pontos A e B, que é justamente o comprimento do segmento AB.

Por Luiz Paulo Moreira
Graduado em Matemática