Posições relativas entre um ponto e uma circunferência

Um pensamento elementar quanto à posição de um ponto em relação a uma circunferência é que esse ponto pode assumir três posições diferentes. Mas como verificar de fato a posição de um ponto no plano cartesiano em relação a uma circunferência cuja equação conhecemos? Para isso precisaremos calcular a distância do ponto até o centro da circunferência ou então substituir esse ponto na equação da circunferência e analisar o resultado obtido.

Antes de iniciarmos essa análise algébrica, vejamos as três posições do ponto:

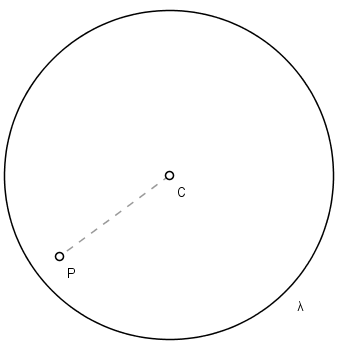
    • O ponto é interno à circunferência. Isso ocorre apenas se a distância do ponto ao centro for menor do que o raio.

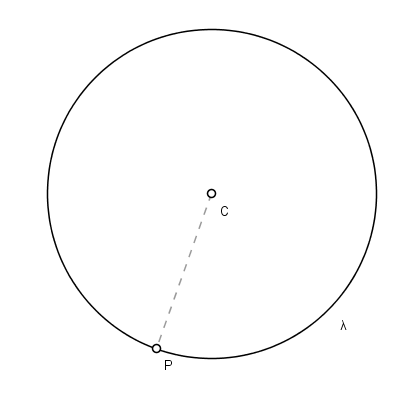
• O ponto pertence à circunferência. Isso ocorre se a distância desse ponto até o centro for igual ao raio.

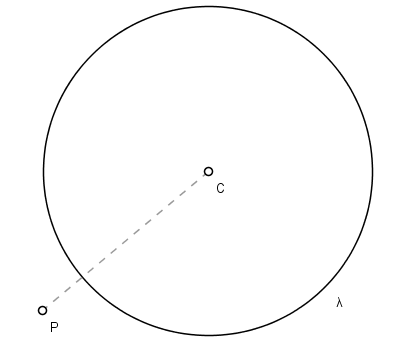
• O ponto é externo à circunferência. Isso ocorre quando a distância do ponto ao centro é maior que o raio.

Sendo assim, quando tivermos que verificar a posição relativa de um ponto em relação a uma circunferência, devemos calcular a distância entre o centro e o ponto, ou então substituir as coordenadas do ponto na equação da circunferência e verificar o valor numérico obtido.

Exemplo:

Quando a equação da circunferência estiver na sua forma reduzida, você não necessita utilizar a fórmula da distância, pois a equação reduzida lhe dá a distância desses dois pontos, basta você resolver o lado esquerdo da igualdade e comparar o resultado ao raio (4²).

• Ponto H (2,3);

Como a distância do ponto H foi igual ao raio, podemos afirmar que esse ponto pertence à circunferência.

• Ponto I (3,3);

Nesse caso, igualamos a 16 esperando que o resultado seja 16 para que o ponto pertença à circunferência, mas ao realizar os cálculos obtemos um valor maior que o raio, por isso o ponto é externo à circunferência.

• Ponto J (3,2);

Mas com analisaríamos o ponto se a equação da circunferência viesse na sua forma geral? O procedimento é bem parecido, entretanto na equação geral não temos uma expressão algébrica igualada ao raio da circunferência. Vejamos a mesma circunferência do exemplo anterior, mas escrita na sua forma geral.

Note que se pegarmos pontos que pertencem à circunferência, a equação acima deverá ser igual a zero. Caso isso não ocorra, o ponto não pertence à circunferência. Vejamos os mesmos pontos do exemplo anterior, porém utilizando a equação geral:

• Ponto H (2,3);

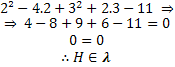
Como a distância do ponto H foi igual ao raio, podemos afirmar que esse ponto pertence à circunferência.

• Ponto I (3,3);

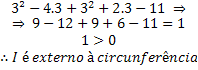
Nesse caso, igualamos a 16 esperando que o resultado seja 16 para que o ponto pertença à circunferência, mas ao realizar os cálculos obtemos um valor maior que o raio, por isso o ponto é externo à circunferência.

• Ponto J (3,2);

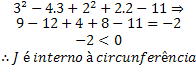
Por Gabriel Alessandro de Oliveira
Graduado em Matemática
Equipe Brasil Escola