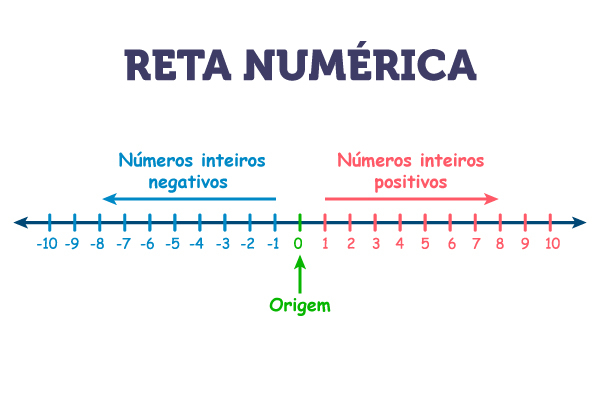
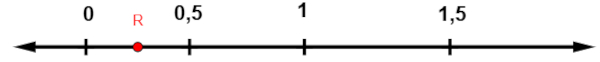A reta numérica é uma maneira de representar graficamente os números reais em uma linha reta, em que cada número corresponde a um ponto específico dela. Com a reta numérica, é possível visualizar melhor as operações básicas e realizar a comparação de valores. A reta numérica tem na sua origem o ponto que representa o número 0. Para a esquerda do 0, estão os números negativos de forma decrescente, e, para a direita do 0, estão os números positivos de forma crescente. Na reta podemos representar qualquer número real, como os números inteiros e os números decimais, sempre entre dois números inteiros.
Leia também: Quais são os conjuntos numéricos?
Tópicos deste artigo
- 1 - Resumo sobre reta numérica
- 2 - Exemplos de reta numérica
- 3 - Características da reta numérica
- 4 - Como construir a reta numérica?
- 5 - Números decimais na reta
- 6 - Exercícios resolvidos sobre reta numérica
Resumo sobre reta numérica
- A reta numérica é uma representação gráfica dos números em uma linha contínua.
- Na reta numérica os números estão organizados em ordem.
- Podemos representar qualquer número real na reta.
- A reta numérica nos auxilia no entendimento das operações e comparação.
Exemplos de reta numérica
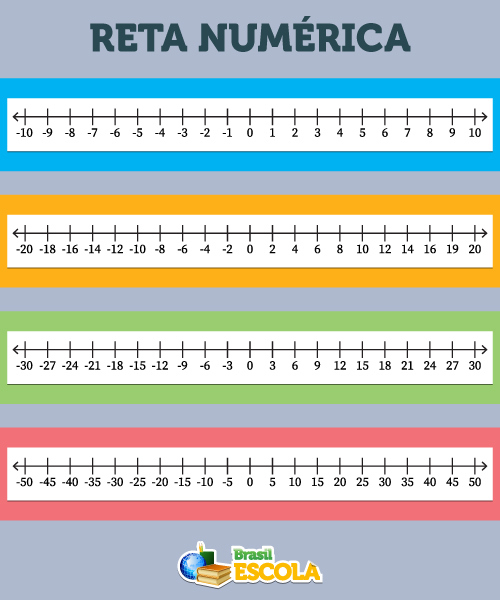
Imprima a reta numérica!
Características da reta numérica
De modo geral, sabemos que a reta numérica tem como principal característica:
- Ponto de origem: geralmente consideramos o 0 como o ponto de origem da reta.
- Infinita: a reta numérica é infinita nos dois lados; logo, representamos uma parte da reta.
- Equidistância: dois números consecutivos têm sempre a mesma distância, definida como a escala da reta numérica.
- Divisível em partes menores: entre dois números, sempre existirá outro número na reta; logo, podemos dividir a reta em partes menores.
Veja também: Diagrama de Venn — outra maneira de representar os conjuntos numéricos
Como construir a reta numérica?
Para construir a reta numérica, é necessário seguir alguns passos, são eles: traçar uma reta horizontal; escolher o ponto central da reta igual ao número 0; determinar a escala, ou seja, se vamos traçar os números de 1 em 1, de 2 em 2, de 0,5 em 0,5; e fazer as marcações dos números de acordo com a escala definida, mantendo sempre a distância entre eles.
-
1º passo: traçar uma reta horizontal
-
2º passo: escolher o ponto central igual a 0
-
3º passo: determinar a escala e fazer as marcações
Nesse caso, faremos de 1 em 1:
Aqui representamos a reta numérica de -6 até 6, mas ela é infinita; logo, é possível representar quantos números forem necessários na reta numérica.
Números decimais na reta
Caso queiramos, podemos representar os números decimais na reta numérica também. Por exemplo, sabemos que, entre 0 e 1, temos o 0,5, que estará no meio entre os dois números:
Cada número decimal pode ser presentado na reta:
Utilizamos o mesmo raciocínio para representar qualquer número decimal. Por exemplo, sabemos que o 0,25 está entre 0 e 0,5, então podemos representá-lo por um ponto, e assim sucessivamente.
Saiba mais: Como fazer operações com números decimais
Exercícios resolvidos sobre reta numérica
Analise a reta numérica a seguir:
![]()
Sobre a reta numérica, podemos afirmar que o número que está exatamente ao meio da distância entre os números -5 e 0 é:
A) -4
B) -3
C) -2
D) -1
Resolução:
Alternativa B
Podemos observar que -3 está a 2 unidades tanto do número -5 quanto do número 0; logo, ele é o número que está exatamente ao meio entre 0 e -5.
Questão 2
A seguir, temos a representação de alguns números na reta numérica:
Analisando a imagem, podemos afirmar que o valor de R é:
A) -0,5
B) 0,25
C) 0,75
D) 1,5
Resolução: Alternativa B
Analisando a imagem, é possível perceber que R está entre 0 e 0,5. O número que se encontra entre 0 e 0,5 é 0,25.
Fontes
IEZZI, Gelson; DOLCE, Osvaldo; DEGENSZAJN, David; PÉRIGO, Roberto; ALMEIDA, Nilze de. Matemática: Ciência e Aplicações – Volume 2. São Paulo: Saraiva, 2018