Posições relativas entre um ponto e uma circunferência

Quanto à circunferência, sabe-se que todos os pontos dela distam igualmente do centro, essa distância igual é denominada de raio. Em comparação com esse raio, ou seja, com os elementos que pertencem à circunferência, podemos ter 3 posições a serem estudadas entre um ponto e uma circunferência.

Para estudar essas posições relativas determinemos uma circunferência λ de centro C(Xc, Yc) e raio r. Analisaremos a posição relativa de um ponto P qualquer em relação a essa circunferência λ.

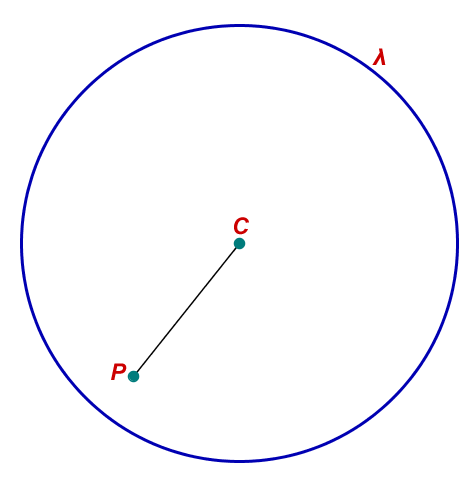
• Ponto P interno à circunferência: isso implica que a distância do ponto P até o centro é menor do que o raio da circunferência. 

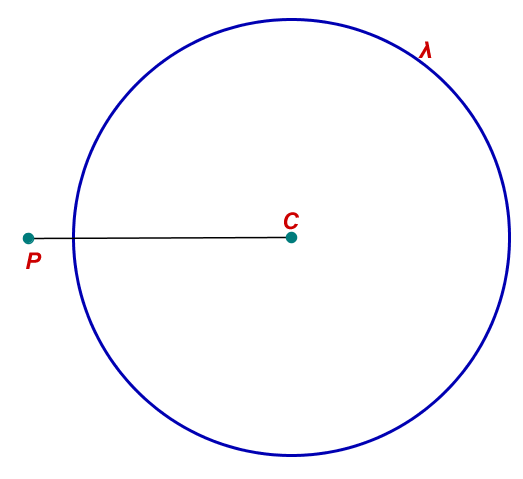
• Ponto P externo à circunferência: neste caso teremos que a distância do ponto P até o centro é maior do que o raio

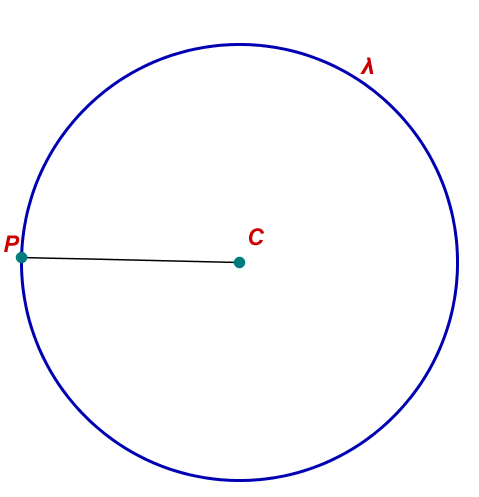
• Ponto P pertence à circunferência: por fim, temos o caso no qual a distância do ponto P ao centro é igual ao raio.

Portanto, quando se conhece o raio da circunferência e deseja-se analisar a posição relativa de um ponto a uma determinada circunferência, basta comparar a distância do Ponto ao centro da circunferência com o valor do raio, feito isso você será capaz de determinar as posições relativas. Com isso é necessário saber como se calcula a distância entre dois pontos, esse estudo você pode acompanhar no artigo Distância entre dois Pontos.

Vejamos algumas situações para realizar esse tipo de análise quanto às posições relativas entre um ponto e uma circunferência.
“Analise as posições relativas entre os pontos dados e a circunferência λ: (x+1)² + (y+1)²=9 , cujos pontos são: A(-2,2). B (-4,1), D(1,1), E(-4,-1)”

Devemos obter duas informações necessárias para realizar os cálculos, que são as coordenadas do Centro da circunferência e o raio, da equação reduzida podemos obter facilmente essas duas informações: C (-1, -1) e raio 3.

Basta calcular as distâncias dos pontos até o centro e comparar com o raio.

Vejamos a representação gráfica das posições relativas desses pontos em relação à circunferência.

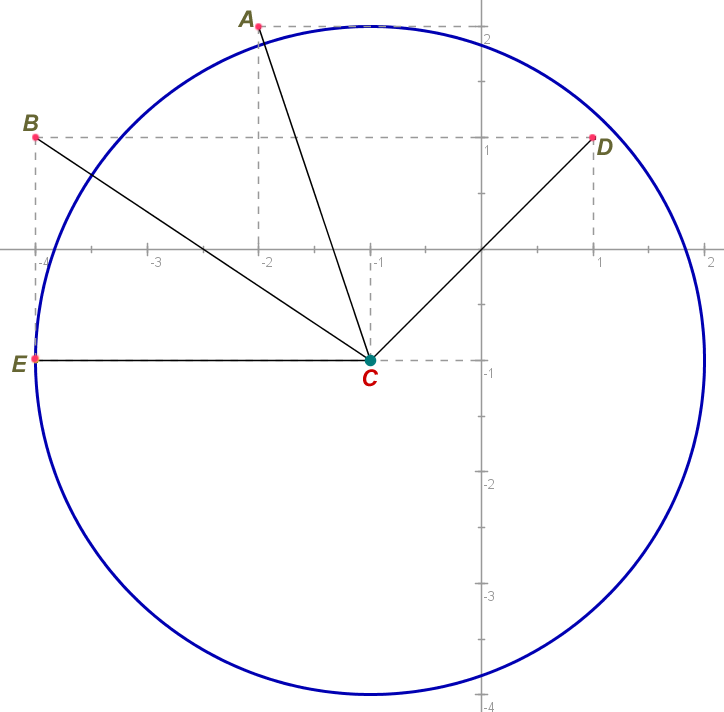
Veja que apenas com o conceito de distância entre pontos foi possível abordar vários temas da geometria analítica. A distância entre pontos está presente em praticamente toda a geometria analítica, se não, em toda ela.

Por Gabriel Alessandro de Oliveira
Graduado em Matemática