O que é função sobrejetora?

Uma função é uma regra que relaciona cada elemento de um conjunto A, chamado de domínio, a um único elemento de um conjunto B, chamado de contradomínio. Além disso, nas funções, o subconjunto do contradomínio que possui todos os elementos relacionados a, pelo menos, um elemento do domínio é chamado de imagem.

As funções podem ser classificadas como injetoras, sobrejetoras ou bijetoras, de acordo com o modo como os elementos do domínio interagem com os elementos do contradomínio. Neste artigo, discutimos o conceito e as características das funções sobrejetoras.

Tópicos deste artigo

• 1 - Conceito de função sobrejetora
• 2 - Função sobrejetora: definição formal
• 3 - Exemplos

Conceito de função sobrejetora

Uma função é considerada sobrejetora quando todos os elementos do seu contradomínio estão relacionados a, pelo menos, um elemento do domínio. Essa definição é equivalente a dizer que o contradomínio de uma função sobrejetora é igual à sua imagem, pois, nesse tipo de função, todo elemento do contradomínio é imagem de algum elemento do domínio.

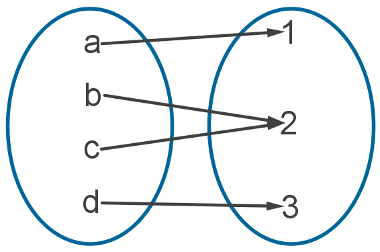
O diagrama a seguir mostra um exemplo de função cujo contradomínio é igual à imagem:

Note que essa função é sobrejetora e que não “sobram” elementos em seu contradomínio, e essa é outra característica das funções sobrejetoras.

Função sobrejetora: definição formal

Considere a função f, com domínio no conjunto A e com contradomínio no conjunto B, definida como f(x) = y. A função f é sobrejetora se, e somente se, para todo y pertencente ao contradomínio B, existe um x pertencente ao conjunto A, tal que f(x) = y. Algebricamente, temos:

Essa simbologia pode ser “traduzida” como: “para todo y pertencente a B, existe x pertencente a A, tal que f(x) = y”.

A outra forma de definir uma função sobrejetora é, dada a função f de domínio A e contradomínio B:

Exemplos

A função f(x) = x, com domínio e contradomínio reais, é sobrejetora porque todo valor de y pertencente ao contradomínio é igual a x pertencente ao domínio.

A função f(x) = x², com domínio e contradomínio reais, não é sobrejetora, pois y pertencente ao contradomínio é positivo, entretanto, existem valores negativos nesse conjunto. Logo, o contradomínio e a imagem dessa função são diferentes.

A função f(x) = x², com domínio e contradomínio iguais ao conjunto dos reais não negativos, é sobrejetora, pois o contradomínio só possui números positivos e o zero e, assim, o contradomínio e a imagem são o mesmo conjunto.

Por Luiz Paulo Moreira
Graduado em Matemática