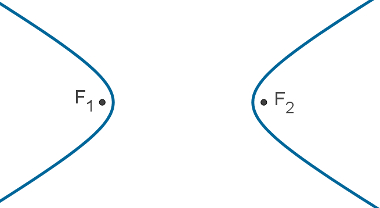O que é hipérbole?

A hipérbole é uma figura geométrica plana formada pela intersecção entre um plano e um cone duplo de revolução. A figura resultante dessa intersecção também pode ser definida algebricamente, a partir da distância entre dois pontos. As hipérboles, embora estejam totalmente contidas em um plano, são curvas. Isso significa que elas não possuem nenhuma parte plana.

A imagem a seguir ilustra uma hipérbole:

Definição formal de hipérbole

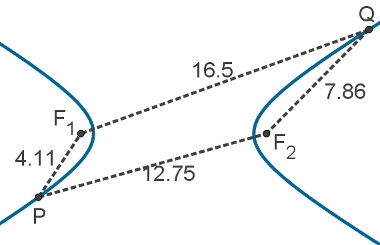
Dados dois pontos do plano, F₁ e F₂, chamados de focos da hipérbole, e a distância 2c entre eles, a hipérbole é o conjunto dos pontos cuja diferença das distâncias até F₁ e até F₂ é igual a uma constante 2a.

Em outras palavras, P é um ponto da hipérbole se |d_PF1 – d_PF2| = 2a. A figura a seguir exemplifica essa definição. Note que a diferença das distâncias entre o ponto Q e os focos é igual à diferença da distância entre o ponto P e os focos.

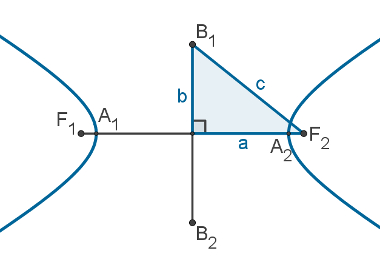
Elementos da hipérbole

Focos: São os pontos F₁ e F₂. A distância entre os focos é 2c e é conhecida como distância focal.

Centro: Dado o segmento cujas extremidades são os focos, o centro da hipérbole é o ponto médio desse segmento.

Eixo real: A hipérbole intercepta o segmento F₁F₂ nos pontos A₁ e A₂. O segmento A₁A₂ é chamado de eixo real. O comprimento do eixo real é 2a.

Eixo imaginário: é o segmento de reta B₁B₂ perpendicular ao eixo real, com ponto médio no centro da hipérbole. A distância do ponto B₁ até A₁ é igual a c, assim como as distâncias de B₁ a A₂, B₂ a A₁ e B₂ a A₂. O comprimento do eixo imaginário é 2b.

Excentricidade: é a razão a seguir

c
a

A seguinte imagem mostra os comprimentos “a”, “b” e “c” em uma hipérbole, na qual é possível observar a relação de Pitágoras:

c² = a² + b²

Equações reduzidas da hipérbole

Existem duas equações reduzidas da hipérbole. A primeira é para o caso em que a hipérbole possui os focos sobre o eixo x e centro sobre a origem de um plano cartesiano:

 x ² –  y ² = 1
a²       b²        

A segunda equação é para o caso em que a hipérbole também possui centro na origem, mas seus focos estão sobre o eixo y do plano cartesiano:

 y ² –  x ² = 1
a²      b²        

Por Luiz Paulo Moreira
Graduado em Matemática

Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:

SILVA, Luiz Paulo Moreira. "O que é hipérbole?"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-hiperbole.htm. Acesso em 30 de novembro de 2021.