Geometria analítica

Geometria analítica é um campo da matemática em que é possível representar elementos geométricos, como pontos, retas, triângulos, quadriláteros e circunferências, utilizando expressões algébricas. As expressões algébricas são derivadas da ideia de união de pontos que seguem determinado padrão. Pontos esses que são dispostos em um sistema de coordenadas proposto por René Descartes.

Saiba mais: Área do triângulo por meio da geometria analítica

Tópicos deste artigo

• 1 - O que a geometria analítica estuda?
• 2 - Conceitos importantes da geometria analítica
  • Distância entre dois pontos
  • Exemplo
  • Coordenadas do ponto médio
  • Exemplo
  • Condição de alinhamento de três pontos
• 3 - Exercícios resolvidos

O que a geometria analítica estuda?

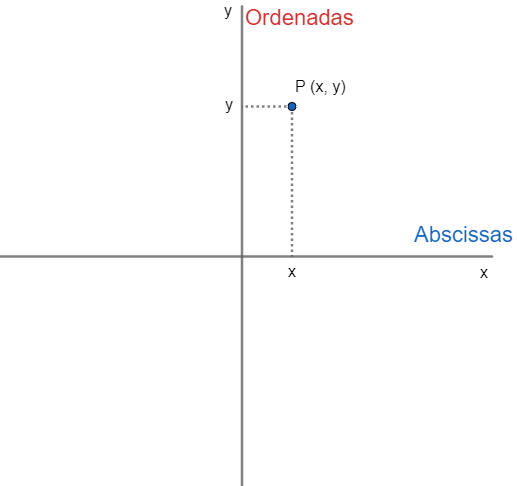
A geometria analítica tem como principal objetivo descrever objetos geométricos utilizando um sistema de coordenadas, o plano cartesiano. Este consiste em dois eixos reais perpendiculares entre si. O eixo horizontal é chamado de eixo das abscissas, e o eixo vertical é chamado de eixo das ordenadas.

Conceitos importantes da geometria analítica

• Distância entre dois pontos

A distância entre os pontos A (x_a, y_a) e B (x_b, y_b) é definida pelo segmento de reta AB, que vamos denotar d_AB. Veja como obter o tamanho desse segmento, ou seja, a distância.

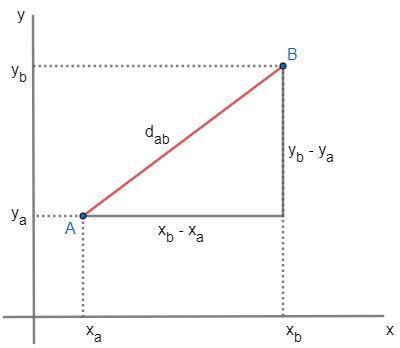
Note que a distância entre os pontos A e B é a hipotenusa do triângulo, logo, para determiná-la, vamos utilizar o teorema de Pitágoras.

• Exemplo

Calcule a distância entre os pontos A (0, 0) e B (4, 2).

Substituindo os valores das coordenadas na fórmula, temos:

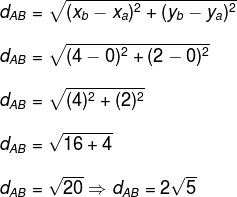
Para aprofundar-se ainda mais nesse conceito da geometria analítica, leia nosso texto: Distância entre dois pontos.

• Coordenadas do ponto médio

Na geometria plana, o ponto médio é o ponto que divide o segmento de reta AB ao meio, ou seja, em duas partes iguais. Na geometria analítica, as coordenadas do ponto médio são dadas por:

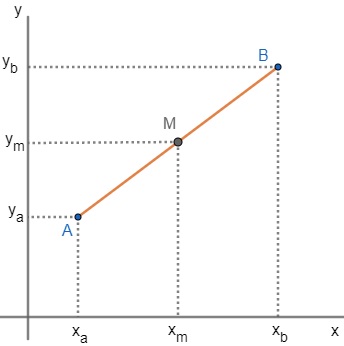
A coordenada do ponto médio, ou seja, do ponto M, é dada por:

• Exemplo

Determine o ponto médio do segmento AB, sabendo que A (2, 1) e B (6, 5).

Substituindo os valores das coordenadas na fórmula, temos:

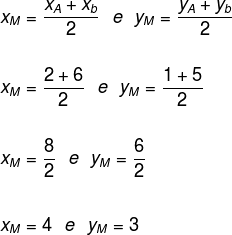
• Condição de alinhamento de três pontos

Considere três pontos — A (x_a, y_a), B (x_b, y_b) e C (x_c, y_c) — distintos no plano. Diremos que os pontos são colineares se o determinante abaixo for igual a zero. Podemos dizer também que eles são colineares se existir uma reta que os contenha.

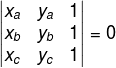
Leia também: Equações com matrizes: como resolver?

Exercícios resolvidos

Questão 1 – (PUC-SP) Os pontos A (3, 5), B (1, -1) e C (x, -16) pertencem a uma mesma reta. Determine o valor de x.

Solução

No enunciado foi dado que os pontos pertencem à mesma reta, ou seja, os pontos A, B e C são colineares. Logo, o determinante é igual a zero.

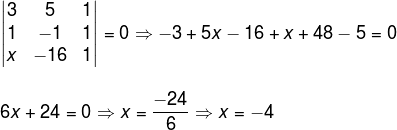
Por Robson Luiz
Professor de Matemática